SOLVERS

One of the most promising aspects of HCL is that general solvers can be written and used on any vector. The same code can be used to solve problems on regular data, irregular data, or any other vector type.

We wrote a routine, NormalSolve, which solves the normal equations,
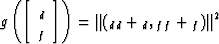. Its arguments include an HCL_LinearOpAdj, , and an
HCL_LinearSolver. An HCL_LinearOpAdj is a linear operator in which the adjoint as well as the forward have been implemented. A HCL_LinearSolver estimates in , when its member function, Solve( L, b, x ) is invoked. NormalSolve is quite general, since it can estimate for any linear operator with adjoint, 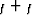, by recasting it into normal form. Typically, we pass HCL's conjugate gradient solver as the solver used by NormalSolve. Finally, since the normal equations are so general, we probably should have written NormalSolve as a HCL_LinearSolver instead of a stand-alone function.

// Solve L'Lx = L'b using a given solver, Slvr (typically cojugate gradient)

void NormalSolve(       HCL_LinearOpAdj  &L,
                  const HCL_Vector       &b,
                        HCL_Vector       &x,
                        HCL_LinearSolver &Slvr )
{
    // Form the normal as a compound linear operator (with adjoint), L'L
    // The zeroes indicate that the caller will delete L and L.Adjoint()
  HCL_CompLinearOpAdj   LtL( (HCL_LinearOpAdj *) & L           , 0 ,
                             (HCL_LinearOpAdj *) &(L.Adjoint()), 0 );
    // Allocate space for L'b
  HCL_Vector          * Ltb = L.Adjoint().Range().Member();

L.Adjoint().Image( b, *Ltb );        // Calculate L'b
  Slvr.Solve( LtL, *Ltb, x );          // Solve L'Lx = L'b   
  delete Ltb;
}

Mark Gockenbach's nonlinear minimization class, HCL_UMin_lbfgs, is quite general and powerful 1996. The user specifies a (real-valued) functional and its gradient. The member function Minimize( f, x ) implements a limited memory Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm to find an 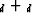which minimizes f. The algorithm is an unconstrained minimization and is especially suited to large-scale problems. We used it successfully to solve a nonlinear missing data problem.