Next: REVIEW OF KNOWN INEQUALITIES
Up: Berryman: Range of the
Previous: WAVE PROPAGATION IN ANISOTROPIC
layercake
Figure 1
Either random or periodic thinly layered elastic materials give rise
to an effective medium characterized by transverse isotropy when the
layers are composed of isotropic elastic materials and the
layer thickness is small compared to the wavelength.

Backus (1962) presents an elegant method of producing the
effective constants for a thinly layered medium composed of
either isotropic or anisotropic elastic layers.
This method applies either to spatially periodic layering
or to random layering, by which we mean either that the material constants
change in a nonperiodic (unpredictable) manner from layer to layer (see Figure 1)
or that the layer thicknesses may also be random.
For simplicity, I will assume that the layers are
isotropic, in which case equation (sscij) becomes
_11_22 _33
_23_31 _12 =
+2& & & & &
& +2& & & &
& & +2& & &
& & & & 2& &
& & & & & 2&
& & & & & & 2
e_11 e_22 e_33
e_23 e_31 e_12 .
The key idea presented by Backus is that these equations
can be rearranged into a form where rapidly varying coefficients
multiply slowly varying stresses or strains. By doing so, I
arrive at the following equation
_11_22 -e_33
e_23e_31 _12 =
4(+)+2 & 2+2
& +2 & & &
2+2 & 4(+)+2
& +2 & & &
+2 & +2
& -1+2 & & &
& & & & 12 & &
& & & & & 12 &
& & & & & & 2
e_11 e_22 _33
_23 _31 e_12 ,
which can be averaged essentially by inspection.
Equation (legtrans) can be viewed as a
Legendre transform of the original equation, to a different
set of dependent/independent variables. Both vectors now
have components with mixed physical significance, some being
stresses and some being strains. Otherwise these equations
are completely equivalent to the original ones.
Performing the layer average, assuming the variation is along the
z or x3 direction, I find, using the notation of (TIss),
<_11><_22> -<e_33>
<e_23><e_31> <_12> =
<4(+)+2>
& <2+2>
& <+2> & & &
<2+2>
& <4(+)+2>
& <+2> & & &
<+2>
& <+2>
& -<1+2> & & &
& & & & <12> & &
& & & & & <12> &
& & & & & & <2>
e_11 e_22 _33
_23 _31 e_12 =
a - f^2/c & b - f^2/c & f/c & & &
b - f^2/c & a - f^2/c & f/c & & &
f/c & f/c & -1/c & & &
& & & 1/2l & &
& & & & 1/2l &
& & & & & 2m
e_11 e_22 _33
_23 _31 e_12 ,
which can then be solved to yield the expressions
a = <+2>^2
<1+2>^-1
+ 4<(+)+2>,
b = <+2>^2
<1+2>^-1
+ 2 <+ 2>,
c = <1+2>^-1
f = <+2>
<1+2>^-1,
l = <1>^-1
and
m = <>.
One very important fact that is known about these equations is that
they reduce to isotropic results with a=c, b=f, and l=m,
if the shear modulus is a constant, regardless of the behavior of 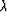 .
.





Next: REVIEW OF KNOWN INEQUALITIES
Up: Berryman: Range of the
Previous: WAVE PROPAGATION IN ANISOTROPIC
Stanford Exploration Project
11/11/1997