




Next: DERIVING AMO AS A
Up: DERIVING AMO AS A
Previous: DERIVING AMO AS A
When the input offset h1 is parallel to
the output offset h2,
the determinant [equation (24)] of the system (23)
is equal to zero.
In this case, as we discussed in the main text,
the 3-D AMO operator degenerates into a 2-D operator.
The fact that the determinant of the system of equations
is equal to zero means that the two equations are linearly dependent,
and that we are left with only one equation.
However, because the operator is two-dimensional,
the number of components of the unknown 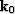 also goes from two to one.
Consequently, another stationary-phase approximation
to the AMO operator can be found.
The new equation is a quartic, and
unfortunately, we have not been able to solve this
new equation analytically.
However, we have found the solution for
the kinematics of the operator with the help of Mathematica;
the resulting expression for the 2-D AMO operator is
presented in equation (3) of the main text.
B
also goes from two to one.
Consequently, another stationary-phase approximation
to the AMO operator can be found.
The new equation is a quartic, and
unfortunately, we have not been able to solve this
new equation analytically.
However, we have found the solution for
the kinematics of the operator with the help of Mathematica;
the resulting expression for the 2-D AMO operator is
presented in equation (3) of the main text.
B





Next: DERIVING AMO AS A
Up: DERIVING AMO AS A
Previous: DERIVING AMO AS A
Stanford Exploration Project
11/11/1997