




Next: 2-D AMO operator
Up: Biondi, Fomel & Chemingui:
Previous: REFERENCES
IN THE FREQUENCY-WAVENUMBER DOMAIN
Our derivation of the AMO operator starts from
the Fourier-domain formulation of DMO
Hale (1984)
and ``inverse'' DMO
Liner (1990); Ronen (1987).
However, because 3-D prestack data is often irregularly sampled,
AMO is most conveniently applied as
an integral operator in the time-space domain.
To derive a time-space representation of the AMO impulse response
from its frequency-wavenumber representation,
we evaluate the stationary-phase approximation of
the inverse Fourier transform along the midpoint coordinates.
The 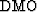 operator and its inverse,
operator and its inverse, 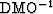 , can be
defined in the zero-offset frequency
, can be
defined in the zero-offset frequency 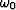 and the midpoint wavenumber
and the midpoint wavenumber 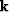 as
as
| 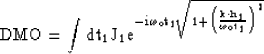 |
(13) |
| 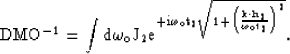 |
(14) |
The 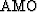 operator is given by the cascades
of
operator is given by the cascades
of 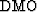 and
and 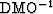 and its impulse response can
can be written as,
and its impulse response can
can be written as,
| 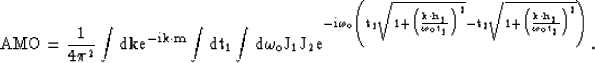 |
(15) |
The derivation of the stationary-phase approximation of the
integral in 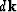 is fairly lengthy and complex.
The following outline
has a similar flavor to the stationary-phase approximation
of the conventional DMO impulse response
presented in Black et al. (1993).
We begin by changing the order of the integrals
and rewriting (15) as
The phase of this integral is,
is fairly lengthy and complex.
The following outline
has a similar flavor to the stationary-phase approximation
of the conventional DMO impulse response
presented in Black et al. (1993).
We begin by changing the order of the integrals
and rewriting (15) as
The phase of this integral is,
| 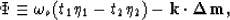 |
(16) |
where,
| 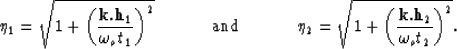 |
(17) |
Next we make the following change of variables and let
| 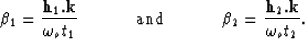 |
(18) |
Therefore, 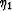 and
and 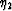 become
become
| 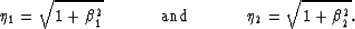 |
(19) |
The derivatives of 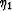 and
and 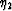 with respect to the
in-line component of the wavenumber kx
and the cross-line component ky can be written as
with respect to the
in-line component of the wavenumber kx
and the cross-line component ky can be written as
| 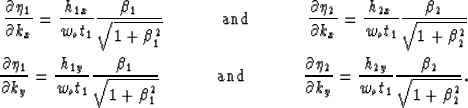 |
|
| (20) |
Making one more change of variables, we let
| 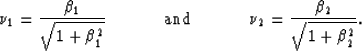 |
(21) |
Setting the derivative of the phase 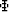 to zero yields the system
of equations:
to zero yields the system
of equations:
| 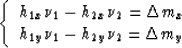 |
(22) |
which we solve for 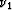 and
and 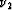 (i.e.,
(i.e., 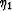 and
and 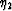 )
at the stationary
path
)
at the stationary
path 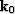 . The determinant of the system is given by
. The determinant of the system is given by
| 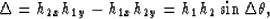 |
(23) |
and the solutions for 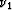 and
and 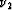 are
are
| 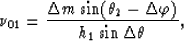 |
(24) |
and
| 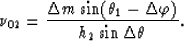 |
(25) |
Now we need to evaluate the phase function 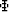 along
the stationary path
along
the stationary path 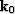 .By respectively multiplying the equations in (23) by
k0x and k0y and summing them together we obtain,
.By respectively multiplying the equations in (23) by
k0x and k0y and summing them together we obtain,
| 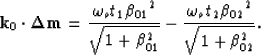 |
(26) |
Substituting this relationship into the expression of the phase
function [equation (17)] we obtain
| 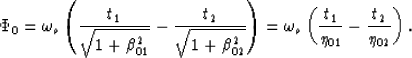 |
(27) |
The phase function along the stationary path is thus
peaked for
| 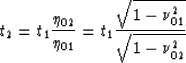 |
(28) |
Substituting equations (25) and (26)
into (29) we obtain (1)
of the main text:
| 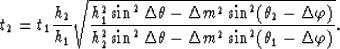 |
(29) |
Next we will derive an expression for the amplitudes of the AMO
impulse response.
The general expression for the stationary-phase approximation
of the 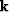 integral in equation (15)
is Bleistein and Handelsman (1975),
integral in equation (15)
is Bleistein and Handelsman (1975),
| 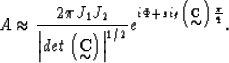 |
(30) |
Therefore we need to evaluate the determinant and the signature
of the curvature matrix 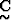 , which is defined as
, which is defined as
| 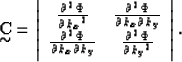 |
(31) |
Taking the second-order partial derivatives of 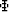 with respect to kx and
ky and using the definitions of
with respect to kx and
ky and using the definitions of 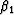 and
and 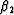 yields
the following expressions for
yields
the following expressions for
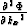 ,
, 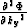 and
and 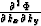 :
:
| 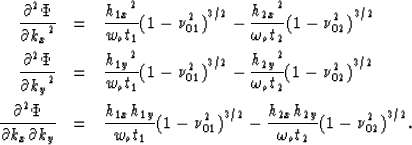 |
(32) |
| (33) |
| (34) |
With a little algebra, one may verify that the determinant of the curvature
matrix is
| 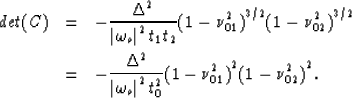 |
|
| (35) |
We notice that the determinant of 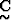 ,which is the product of the two eigenvalues of
,which is the product of the two eigenvalues of 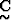 ,is always negative,
that is; that the two eigenvalues have opposite signs
and thus the signature of
,is always negative,
that is; that the two eigenvalues have opposite signs
and thus the signature of 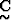 ,which is defined as the number of
positive eigenvalues minus the number of negative eigenvalues,
is always null.
Therefore, the second term
of the phase shift in equation (31) vanishes.
,which is defined as the number of
positive eigenvalues minus the number of negative eigenvalues,
is always null.
Therefore, the second term
of the phase shift in equation (31) vanishes.
To obtain expressions for the AMO amplitude,
we need to substitute equation (36)
in equation (31),
together with the corresponding expressions
for J1 and J2.
For the Jacobian J1 of the forward DMO
we can use any of the Jacobians proposed in the literature
by Hale 1984,
Zhang and Black 1988,
and Bleistein 1990.
The Jacobian J2 of inverse DMO
can be derived with Beylkin's theory
for the asymptotic inverse of stacking operators
Beylkin (1985); Cohen and Hagin (1985).
The expression for the Jacobian of the
asymptotic inverse for Hale's DMO were derived
by Liner and Cohen 1988.
Chemingui and Biondi 1995 and
Fowler (personal communication) independently derived
the inverse for Zhang-Black's DMO.
As mentioned in the main text, we used Zhang-Black's Jacobians
for the actual application of AMO; that is,
| 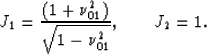 |
(36) |
Finally,
after taking into account he Jacobian of the transformation
from t1 to t0 (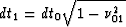 )in the first integral of
equation (16),
we can write the amplitude term for the AMO integral:
)in the first integral of
equation (16),
we can write the amplitude term for the AMO integral:
| 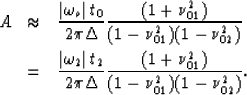 |
(37) |
| (38) |
The last substitution, 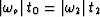 ,enables us to apply the differentiation operator
,enables us to apply the differentiation operator
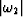 to the output data;
it is correct because t0 and t2 are linked
by the linear relationship
to the output data;
it is correct because t0 and t2 are linked
by the linear relationship
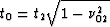 .
.
The expression for the amplitudes presented
in equation (4) of the main text
follows by simple substitution of
the expressions for 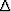 ,
, 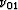 ,and
,and 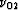 , from equations (24), (25) and (26)
into equation (39).
, from equations (24), (25) and (26)
into equation (39).





Next: 2-D AMO operator
Up: Biondi, Fomel & Chemingui:
Previous: REFERENCES
Stanford Exploration Project
11/11/1997
![]() operator and its inverse,
operator and its inverse, ![]() , can be
defined in the zero-offset frequency
, can be
defined in the zero-offset frequency ![]() and the midpoint wavenumber
and the midpoint wavenumber ![]() as
as
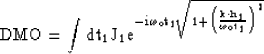
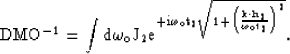
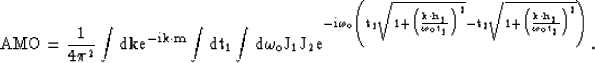
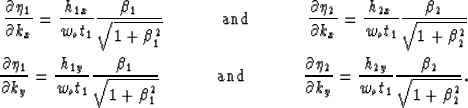
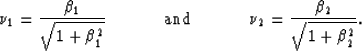
![]() integral in equation (15)
is Bleistein and Handelsman (1975),
integral in equation (15)
is Bleistein and Handelsman (1975),
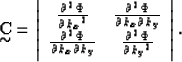
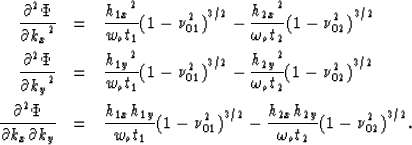
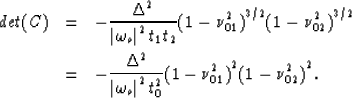
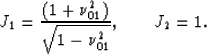
![]() )in the first integral of
equation (16),
we can write the amplitude term for the AMO integral:
)in the first integral of
equation (16),
we can write the amplitude term for the AMO integral:
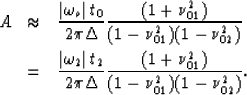
![]() ,
, ![]() ,and
,and ![]() , from equations (24), (25) and (26)
into equation (39).
, from equations (24), (25) and (26)
into equation (39).