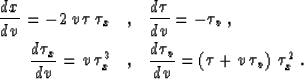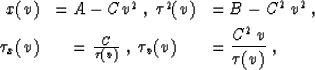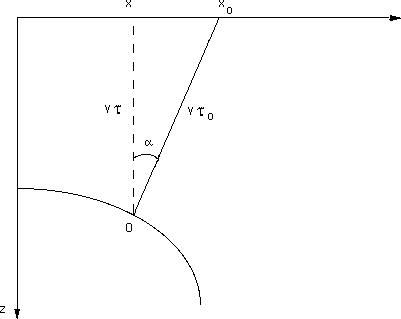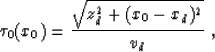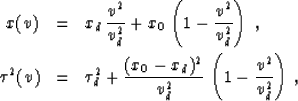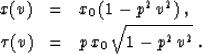Next: Kinematics of Residual NMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: KINEMATICS OF VELOCITY CONTINUATION
The kinematic equation for zero-offset velocity continuation is
| 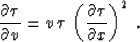 |
(2) |
The typical boundary problem associated with it is to find the
traveltime surface 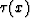 for a constant velocity v, given the
traveltime surface
for a constant velocity v, given the
traveltime surface 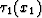 at some other velocity v1. Both
surfaces correspond to the reflector images obtained by time
migrations with the specified velocities. When the migration velocity
approaches zero, post-stack time migration approaches the identity
operator. Therefore, the case of v1 = 0 corresponds kinematically
to the zero-offset (post-stack) migration, and the case of v = 0
corresponds to the zero-offset modeling (demigration).
at some other velocity v1. Both
surfaces correspond to the reflector images obtained by time
migrations with the specified velocities. When the migration velocity
approaches zero, post-stack time migration approaches the identity
operator. Therefore, the case of v1 = 0 corresponds kinematically
to the zero-offset (post-stack) migration, and the case of v = 0
corresponds to the zero-offset modeling (demigration).
The appropriate mathematical method of solving the kinematic
problem posed above is the method of characteristics Courant (1962). The
characteristics of equation (2) are the trajectories
followed by individual points of the reflector image in the velocity
continuation process, which I have called velocity rays
Fomel (1994). Velocity rays are defined by the system of ordinary
differential equations derived from (2) according to the
classic rules of mathematical physics:
| 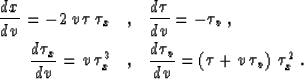 |
(3) |
| (4) |
An additional constraint for the quantities 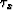 and
and 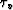 follows from equation (2), rewritten in the form
follows from equation (2), rewritten in the form
| 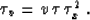 |
(5) |
One can easily solve the system of equations (3) and (4) by the classic
mathematical methods for the ordinary differential equations. The
general solution of the system takes the parametric form
| 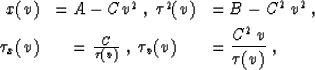 |
(6) |
| (7) |
where A, B, and C are constant along each individual velocity
ray. These three constants are determined from the boundary conditions
as
| 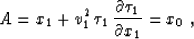 |
(8) |
| 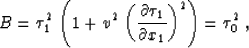 |
(9) |
| 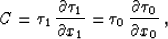 |
(10) |
where 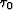 and x0 correspond to the zero velocity (unmigrated
section). Equations (8), (9), and (10) have a clear
geometric meaning illustrated in Figure 1. Noting the
simple relationship between the midpoint derivative of the vertical
traveltime and the local dip angle
and x0 correspond to the zero velocity (unmigrated
section). Equations (8), (9), and (10) have a clear
geometric meaning illustrated in Figure 1. Noting the
simple relationship between the midpoint derivative of the vertical
traveltime and the local dip angle  (appendix A),
(appendix A),
| 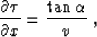 |
(11) |
we can see that equations (8) and (9) are precisely equivalent
to the evident geometric relationships
| 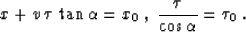 |
(12) |
Equation (10) states that the points on a velocity ray correspond
to a single reflection point, constrained by the values of  ,v, and
,v, and  . As follows from equations (6), the
projection of a velocity ray to the time-midpoint plane has the
parabolic shape
. As follows from equations (6), the
projection of a velocity ray to the time-midpoint plane has the
parabolic shape 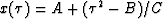 , which has been
noticed by Chun and Jacewitz 1981. On the
depth-midpoint plane, the velocity rays have the circular shape
, which has been
noticed by Chun and Jacewitz 1981. On the
depth-midpoint plane, the velocity rays have the circular shape
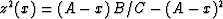 , described by Liptow and Hubral
1995 as ``Thales circles.''
, described by Liptow and Hubral
1995 as ``Thales circles.''
vlczor
Figure 1 Zero-offset reflection in a constant
velocity medium (a scheme).
|
| 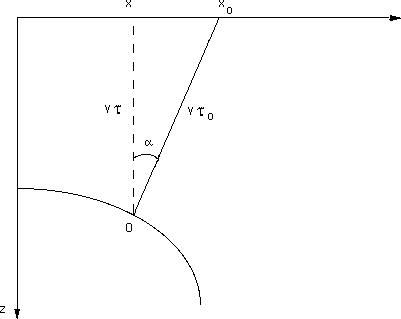 |

For an example of kinematic continuation by velocity rays, let us
consider the case of a point diffractor. If the diffractor location in
the subsurface is the point xd,zd, then the reflection traveltime at
zero offset is defined from Pythagoras's theorem as the hyperbolic
curve
| 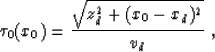 |
(13) |
where v is half of the actual velocity. Applying formulas
(6), we can deduce that the velocity rays in this case have the
following mathematical expressions:
| 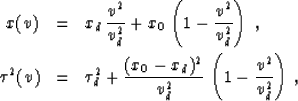 |
(14) |
| (15) |
where 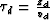 .Eliminating x0 from the system of equations (14) and
(15) leads to the expression for the velocity continuation
``wavefront'':
.Eliminating x0 from the system of equations (14) and
(15) leads to the expression for the velocity continuation
``wavefront'':
| 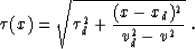 |
(16) |
For the case of a point diffractor, the wavefront corresponds precisely
to the summation path of the residual migration operator
Rothman et al. (1985). It has a hyperbolic shape when vd > v
(undermigration) and an elliptic shape when vd < v
(overmigration). The wavefront collapses to a point when the velocity
v coincides with the actual effective velocity vd. At zero
velocity, v=0, the wavefront takes the familiar form of the post-stack migration
hyperbolic summation path. The form of the velocity rays and wavefronts
is illustrated in the left plot of Figure 2.
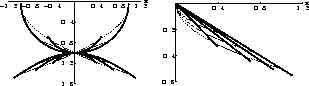
vlcvrs
Figure 2 Kinematic
velocity continuation in the post-stack migration domain. Solid lines
denote wavefronts: reflector images for different migration
velocities; dashed lines denote velocity rays. Left: the case of a
point diffractor. Right: the case of a dipping plane reflector.





Another important example is the case of a dipping plane
reflector. For simplicity, let us put the origin of the midpoint
coordinate x at the point of the plane intersection with the surface
of observations. In this case, the plane reflector has the simple
expression
| 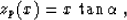 |
(17) |
where  is the dip angle. The zero-offset reflection traveltime
is the plane with a changed angle. It can be expressed as
is the dip angle. The zero-offset reflection traveltime
is the plane with a changed angle. It can be expressed as
| 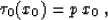 |
(18) |
where 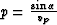 , and vp is the half of the
actual velocity. Applying formulas (6) leads to
the following parametric expression for the velocity rays:
, and vp is the half of the
actual velocity. Applying formulas (6) leads to
the following parametric expression for the velocity rays:
| 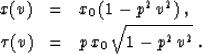 |
(19) |
| (20) |
Eliminating x0 from the system of equations (19) and (20)
shows that the velocity continuation wavefronts are planes with a
modified angle:
| 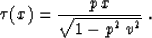 |
(21) |
The right plot of Figure 2 shows the geometry of the
kinematic velocity continuation for the case of a plane reflector.





Next: Kinematics of Residual NMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: KINEMATICS OF VELOCITY CONTINUATION
Stanford Exploration Project
11/12/1997