




Next: Conclusions
Up: Fomel & Grechka: Nonhyperbolic
Previous: Curved reflector in a
In a simple model with one horizontal reflector, the anisotropic
effect of the group velocity changing with the angle of propagation is
somewhat similar to the effect of lateral heterogeneity. In this
section, we address the question of whether nonhyperbolic moveout in
isotropic weakly heterogeneous model can mimic that in a homogeneous
weakly anisotropic model. The analysis follows the results of Grechka
1996.
The angle dependence of the group velocity in formulas (1) and
(9) is characterized by small anisotropic
coefficients. Therefore, we can assume that an analogous effect of
lateral heterogeneity might be cause by a small velocity
perturbation. The appropriate model is a laterally heterogeneous (LH)
medium with velocity
| ![\begin{displaymath}
V(x) = V_0\,\left[ 1 + c(x) \right]\;,\end{displaymath}](img104.gif) |
(85) |
where 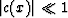 is a dimensionless function. The velocity
function in formula (85) has the generic perturbation form that
allows us to use the tomographic linearization assumption. That is, we
neglect the ray bending caused by the small velocity perturbation c
and compute the perturbation of traveltimes along straight rays in the
constant velocity V0. Thus, we can rewrite equation (13)
for this case as
is a dimensionless function. The velocity
function in formula (85) has the generic perturbation form that
allows us to use the tomographic linearization assumption. That is, we
neglect the ray bending caused by the small velocity perturbation c
and compute the perturbation of traveltimes along straight rays in the
constant velocity V0. Thus, we can rewrite equation (13)
for this case as
| 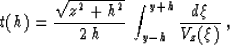 |
(86) |
where y is the midpoint location, and the integral limits correspond
to the source and receiver locations. For simplisity, and without loss
of generality, we can set y to zero. Linearizing with respect to the
small perturbation c(x), we get
| ![\begin{displaymath}
t(h) = { \sqrt{z^2 + h^2} \over V_0 } \left[ 1 - {1 \over {2\,h}}
\int_{-h}^{h} c(\xi) d\xi \right]\;.\end{displaymath}](img107.gif) |
(87) |
From the form of equation (87) it is clear that lateral
heterogeneity can cause many different types of nonhyperbolic moveout
shapes. In particular, comparing equations (87) and
(15), we conclude that a pseudo-anisotropic behavior of
traveltimes is caused by lateral heterogeneity of the form
| ![\begin{displaymath}
c(h) = { d \over {d h}}
\left[{ {h^3 (h^2 \epsilon + z^2 \delta )} \over
{(h^2 + z^2)^2} } \right]\end{displaymath}](img108.gif) |
(88) |
or, in the linear approximation,
| ![\begin{displaymath}
c(h) = \left[\delta\,t_0^2\,V_n^2\,h^2\,(3 t_0^2 V_n^2 - h^2...
...0^2 V_n^2 + h^2) \right] /
\left(t_0^2 V_n^2 + h^2 \right)^3\;,\end{displaymath}](img109.gif) |
(89) |
where  and
and  should be considered now as the
parameters of the isotropic lateral heterogeneous velocity
field. Equation (89) indicates that the velocity heterogeneity
c(x), reproducing moveout (16) in a homogeneous TI medium,
is the symmetric function of the offset h. It is not surprising
because the velocity function (1), corresponding to transverse
isotropy, is symmetric as well.
should be considered now as the
parameters of the isotropic lateral heterogeneous velocity
field. Equation (89) indicates that the velocity heterogeneity
c(x), reproducing moveout (16) in a homogeneous TI medium,
is the symmetric function of the offset h. It is not surprising
because the velocity function (1), corresponding to transverse
isotropy, is symmetric as well.
For more details on the relation between lateral heterogeneity and
transevse isotropy in interpreting P-wave reflection moveout, see
Grechka (1996).





Next: Conclusions
Up: Fomel & Grechka: Nonhyperbolic
Previous: Curved reflector in a
Stanford Exploration Project
11/12/1997