




Next: EXAMPLES
Up: Fomel: Conjugate directions
Previous: Short memory of the
The following ratfor program, cdstep(), implements one iteration
of the conjugate-direction method. It is based upon Jon Claerbout's
cgstep() program Claerbout (1994) and uses an analogous
naming convention. Vectors in the data space are denoted by double
letters.
# A step of conjugate-direction descent.
#
subroutine cdstep( niter,iter, n, x, g, s, m, rr, gg, ss,ssn)
integer i,j,liter, niter,iter, n, m
real x(n), rr(m), # solution, residual
g(n), gg(m), # direction, conjugate direction
s(n,niter), ss(m,niter) # step, conjugate step
double precision ddot, alpha, ssn(niter)
liter = min0(iter,niter)
do i= 1, n # initial direction
s(i,liter) = g(i)
do i= 1, m
ss(i,liter) = gg(i)
do j= 1, liter-1 { # update direction
alpha = ddot(m,gg,ss(1,j))/ssn(j)
do i= 1, n
s(i,liter) = s(i,liter) - alpha * s(i,j)
do i= 1, m
ss(i,liter) = ss(i,liter) - alpha * ss(i,j)
}
ssn(liter) = dmax1(ddot(m,ss(1,liter),ss(1,liter)),1.d-35)
if (liter == niter) {
do j= 1, niter-1 {
ssn(j) = ssn(j+1)
do i= 1, n
s(i,j) = s(i,j+1)
do i= 1, m
ss(i,j) = ss(i,j+1)
}
}
alpha = ddot(m,ss(1,liter),rr)/ssn(liter)
do i= 1, n # update solution
x(i) = x(i) + alpha * s(i,liter)
do i= 1, m # update residual
rr(i) = rr(i) - alpha * ss(i,liter)
return; end
double precision function ddot( n, x, y)
integer i, n; real x(n), y(n); double precision val
val = 0.; do i=1,n { val = val + x(i) * y(i) }
ddot = val; return; end
In addition to the previous steps 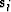 (array
(array
s) and their conjugate counterparts 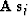 (array
(array
ss), the program stores the squared norms 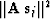 (array
(array ssn) to avoid recomputation.
For practical reasons, the number of remembered iterations
niter can actually be smaller than the total number of
iterations. The value niter=2 corresponds to the
conjugate-gradient method. The value niter=1 corresponds to the
steepest-descent method. The iteration process should start with
iter = 1, corresponding to the first steepest-descent iteration
in the method of conjugate gradients.





Next: EXAMPLES
Up: Fomel: Conjugate directions
Previous: Short memory of the
Stanford Exploration Project
11/12/1997