




Next: MEDIANS IN AUTOREGRESSION
Up: Claerbout: Medians in regression
Previous: INTRODUCTION
Let ri be components of a residual vector  and consider perturbation components
and consider perturbation components 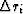 .We study the properties of the new residual
.We study the properties of the new residual
| 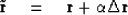 |
(1) |
where  is a scaling factor.
Consider the implications of
is a scaling factor.
Consider the implications of
|  |
(2) |
| (3) |
Thus choosing
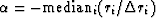 causes
the median of
causes
the median of 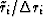 to vanish
which means
to vanish
which means 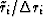 has as many positive terms
as negative ones.
Consequently, the number of polarity agreements
in the component pairs
has as many positive terms
as negative ones.
Consequently, the number of polarity agreements
in the component pairs 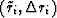 of the new residual
of the new residual 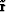 and the regressor
and the regressor 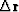 equals their polarity disagreements.
In other words,
equals their polarity disagreements.
In other words,
| 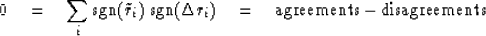 |
(4) |
In what sense have we created the smallest new residual 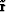 ?
It is smallest in the sense that if we change
?
It is smallest in the sense that if we change 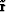 by adding or subtracting some
by adding or subtracting some  of the perturbation
of the perturbation 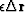 ,the count of growing components less the decreasing components
of
,the count of growing components less the decreasing components
of 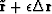 is
is
| 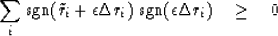 |
(5) |
The best residual is one in which any perturbation
serves only to increase the polarity agreements with the regressor.
We chose  to reduce as many components
of
to reduce as many components
of 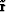 as we could.
as we could.





Next: MEDIANS IN AUTOREGRESSION
Up: Claerbout: Medians in regression
Previous: INTRODUCTION
Stanford Exploration Project
11/12/1997
![]() and consider perturbation components
and consider perturbation components ![]() .We study the properties of the new residual
.We study the properties of the new residual
