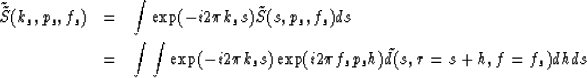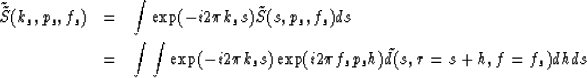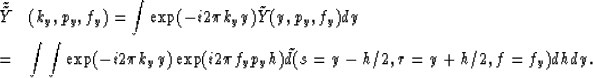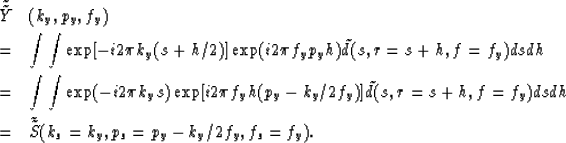Conversion of midpoint to source gather

Fortunately, we can convert this common-midpoint transform (9) into an equivalent common-source transform (6). Let us make two additional Fourier transforms over spatial dimensions of s and y for the spatial frequencies k_s and k_y:

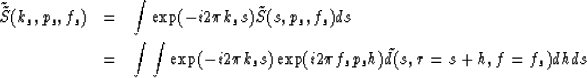$$\begin{eqnarray} \tilde {\tilde S} (k_s, p_s, f_s) &=& \int \exp( -i 2 \pi k_s ... ...k_s s ) \exp( i 2 \pi f_s p_s h ) \tilde d (s,r=s+h,f=f_s) dh ds\end{eqnarray}$$ (10)

and

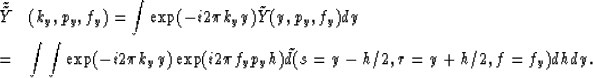$$\begin{eqnarray} &\tilde {\tilde Y}& (k_y, p_y, f_y) = \int \exp( -i 2 \pi k_y ... ...exp( i 2 \pi f_y p_y h ) \tilde d (s=y-h/2,r=y+h/2,f=f_y ) dh dy .\end{eqnarray}$$ (11)

To place the second integral (11) in the form of the first (10), we should change the variables of integration from h and y to h and s. (The Jacobian of this transformation is 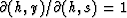$\partial(h,y)/\partial(h,s)=1$.) Substituting y=s+h/2 we get

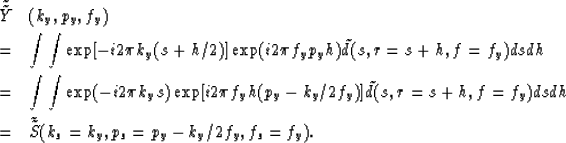$$\begin{eqnarray} &\tilde {\tilde Y}& (k_y, p_y, f_y) \nonumber\\ &=& \int \int \... ...tilde {\tilde S} ( k_s = k_y , p_s = p_y - k_y/2f_y , f_s = f_y) .\end{eqnarray}$$ (12)

Thus, a two-dimensional stretch of the midpoint-gather transform becomes equivalent to the source-gather transform. For a given dip over offset in a midpoint gather p_y, we can identify a dip over midpoint

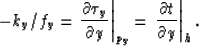$$- k_y/f_y = \left. {\partial \tau_y \over \partial y}\right\vert _{p_y} = \left. {\partial t \over \partial y}\right\vert _h .$$ (13)

The adjustment of p_s = p_y - k_y/2f_y subtracts half of this midpoint dip from the offset dip. With a careful application of the chain rule, and carefully distinguishing partial derivatives, we could arrive at the same result

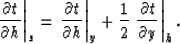$$\left. {\partial t \over \partial h}\right\vert _s = \left.... ...1 \over 2} \left. {\partial t \over \partial y}\right\vert _h .$$ (14)