INTRODUCTION

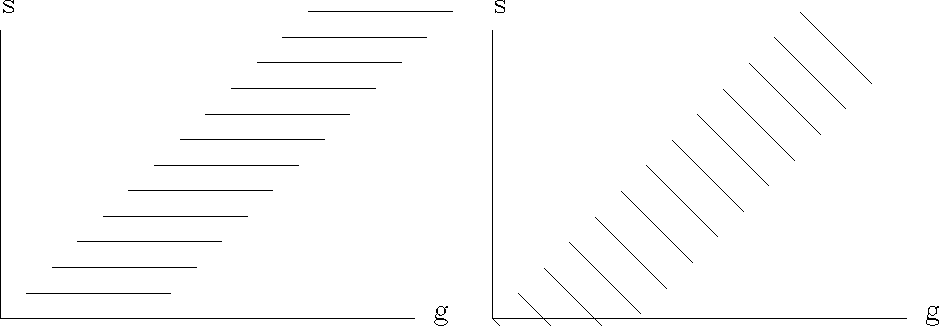Our fundamental goal is to downward continue seismic data accurately and economically thru media where the velocity v(x,z) is laterally variable. A few slant stacks and the wave equation meet the economy requirement. Tieman's transformation described here should greatly reduce the numerical noise generated by insufficient data density.

Slant stacks over shot point on common geophone gathers simulate plane waves entering the earth. Because of the reciprocal principle, the same is true for common shot gathers. As we will see, practical difficulties arise with slant stacks on common shot gathers and common geophone gathers that do not arise on common midpoint gathers. Figure 1 shows the familiar definitions.

 

sg Figure 1 Lines on the left denote shot profiles (CSP). On the right lines denote common midpoint gathers (CMG).

To illustrate the distinction of the two types of gathers for the purpose of slant stacking, I prepared travel time curves for an earth model of random dipping planes. The random dip angles were taken to be uniformly distributed in the range $\pm 45^\circ$.

• On the common shot gather we see the wavefields expanding from an ``image source''. Since the wavefronts are circular, the travel time curves are hyperbolas, each with its top above the image source. (This is because circles and hyperbolas are slices from the conic section v²t²=(x-x₀)²+(z-z₀)².) All curves have the same asymptotic slope 1/v. The hyperbolas truncate where the dipping bed hits the surface.
• On the common midpoint gather we see the result generally attributed to Frank Levin, that there are hyperbolas all topping at zero offset, but with asymptotic velocities higher than the earth velocity by the cosine of the dip.

The travel time equations are found in most any textbook on reflection seismology, such as IEI. I plot the result in Figure 2.

 

tieman Figure 2 Seismic arrival times on an earth of random dipping planes. Left is for CSP. Right is for CMG.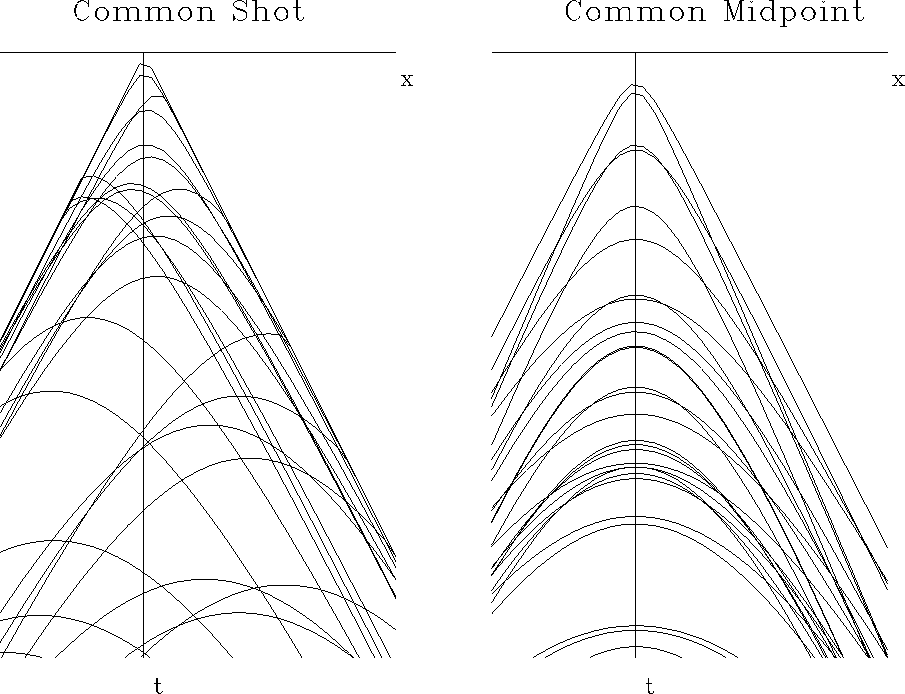

The important thing to notice in Figure 2 is that on the common midpoint gather the data slopes are highly predictable, all lying within a small range, whereas the slopes on the common shot or common geophone gather cover a wide range. The unpredictable slopes create a problem for slant stacking because they demand a much greater spatial density of data to avoid spatial aliasing.

Tieman's contribution is to provide us with a transformation from a slant stack at a single constant stepout p at common midpoint, performed at all midpoints, to a slant stack at a constant stepout p (different p ?) for each of all the shot points (or geophone points).