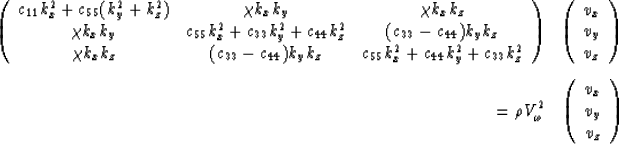Next: Plane wave modes
Up: TRANSVERSE ISOTROPY
Previous: TRANSVERSE ISOTROPY
The elastic modulus matrix of an HTI medium with a symmetry axis along
the x direction (which I will denote as 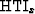 ) has the
following form (in compressed notation):
) has the
following form (in compressed notation):
| 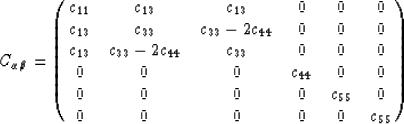 |
(3) |
This representation can easily be obtained by a 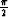 rotation of the VTI's elastic matrix along the y axis. Incorporating
this expression into equation (1) and identifying
rotation of the VTI's elastic matrix along the y axis. Incorporating
this expression into equation (1) and identifying 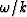 as the velocity
as the velocity 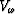 of the plane wave with propagation
direction (kx,ky,kz) gives us
of the plane wave with propagation
direction (kx,ky,kz) gives us
| 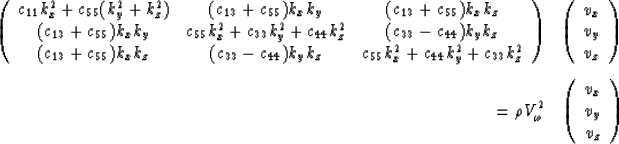 |
|
| (4) |
| |
From here on, to simplify notation, I use the variables
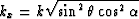
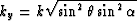 and
and 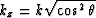 , introduced by Dellinger 1991. Thus
we rewrite equation (4) as
, introduced by Dellinger 1991. Thus
we rewrite equation (4) as
| 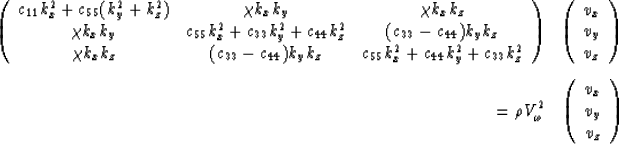 |
|
| (5) |
| |
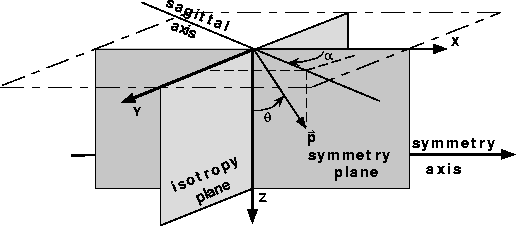
HTIprop
Figure 1 Definition of propagation
angles. The azimuthal angle  is measured with respect to the
symmetry axis, and the incidence angle is measured with respect to the
symmetry axis, and the incidence angle 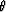 with respect to the
vertical axis. with respect to the
vertical axis.
|
|  |






Next: Plane wave modes
Up: TRANSVERSE ISOTROPY
Previous: TRANSVERSE ISOTROPY
Stanford Exploration Project
11/12/1997
![]() ) has the
following form (in compressed notation):
) has the
following form (in compressed notation):
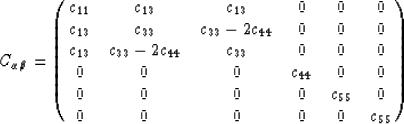
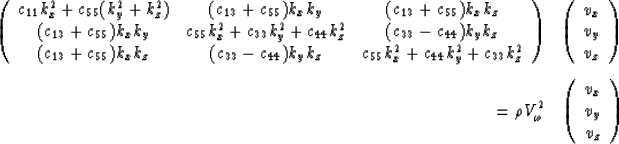
![]()
![]() and
and ![]() , introduced by Dellinger 1991. Thus
we rewrite equation (4) as
, introduced by Dellinger 1991. Thus
we rewrite equation (4) as