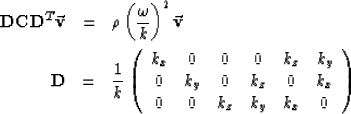
When considering plane waves propagating in a homogeneous anisotropic medium, it is convenient to use the Christoffel equation. This equation is simply the elastodynamic wave equation Fourier transformed over space and time. It specifies the propagation velocity and particle-motion (also called polarization) direction for each plane-wave component in the Fourier domain. The Christoffel equation takes the form of a simple eigenvalue-eigenvector problem, as follows:
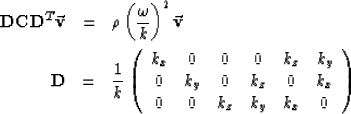 |
(1) | |
Solving the eigensystem in equation (1) is straightforward.
For any wavenumber vector ![]() , the symmetry of the matrix
, the symmetry of the matrix
![]() ensures that the underlying
eigenvalue-eigenvector problem is well-behaved: we can always
find three distinct modes associated with three orthogonal directions
of particle motion. This eigensystem has solutions only when its
determinant vanishes:
ensures that the underlying
eigenvalue-eigenvector problem is well-behaved: we can always
find three distinct modes associated with three orthogonal directions
of particle motion. This eigensystem has solutions only when its
determinant vanishes:
![]()
| |
(2) |
The three roots, which correspond to the eigenvalues of equation (1) are the velocities of the three fundamental plane waves. The eigenvectors of equation (1) are, respectively, the three directions of particle motion. In general, none of these fundamental waves will be purely longitudinal or purely transverse.