TIEMANS'S TRANSFORM

Tieman's sequence of transformation equations ideally applies to a world defined by continuous infinite functions of space and time. The use of two dimensional Fourier transforms in this method, both in the forward and inverse sense, indicate that there may be resolution questions and artifacts to deal with when this transform is applied to finite spaces, not to mention boundary effects inevitable with the slant stack. Precision of the two Fourier transformed axis, the retarded time axis, $\tau$, and the midpoint axis, y, is important for the Tieman method because the transformation involves a shift of the third axis, the Snells parameter axis, p, as a function of the Fourier transformed axis. This is evident in the relation of Snells parameter in the shot domain to Snells parameter in the midpoint domain. The following is the Tieman transformation where the   represents a Fourier transform and Y and S represent the slant stack of the the cmp gather and the slant stack of the shot gather respectively. This notation follows the convention of Harlan and Claerbout1996.

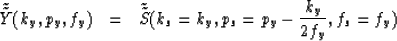$$\begin{eqnarray} \tilde{\tilde{Y}}(k_{y},p_{y},f_{y}) &=& \tilde{\tilde{S}}(k_{s}=k_{y}, p_{s}=p_{y} - \frac{k_{y}}{2f_{y}},f_{s}=f_{y})\end{eqnarray}$$ (2)

Dense sampling of the time axis is often achieved in real data situations, but the midpoint axis and offset axis will, in most cases be sampled much less. Coarse sampling in the midpoint axis could be problematic, especially if the sampling is such that dips evaluated by the 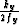$\frac{k_{y}}{2f_{y}}$ factor in the Tieman transformation are aliased. If the transformation is applied to unmigrated data, diffraction events could create confusing dips which could be significant to the shift equation. Aliasing due to coarse sampling along the offset axis of the cmp gather will also limit the accuracy of the transform, though not to the degree that aliasing would effect the direct application of a slant stack to the corresponding shot gather Harlan and Claerbout (1996).