Next: Datuming by wavefield depth
Up: Unitarity of the depth
Previous: Unitarity of the depth
The split-step Fourier extrapolation Stoffa and Fokkema (1990)
consists of two-step extrapolation, which is
a phase shifting in the 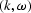 domain
followed by an additional phase shifting
in the
domain
followed by an additional phase shifting
in the 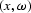 domain.
domain.
Let us consider a simple case that consists
of two depth levels of extrapolation.
Then the forward operator can be expressed as follows:
| 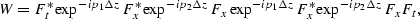 |
(55) |
where Fx and Ft represent the Fourier transform
along the space and the time domains, respectively.
The phases p1 and p2 quantify the amount of phase shift
in the 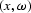 and in the
and in the 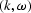 domain,
and are defined as follows:
domain,
and are defined as follows:
| 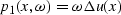 |
(56) |
and
| 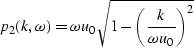 |
(57) |
where u0 represents the reference slowness
and 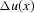 is a variation
of the slowness from the reference slowness.
Then the adjoint of the forward operator becomes
is a variation
of the slowness from the reference slowness.
Then the adjoint of the forward operator becomes
| 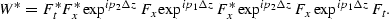 |
(58) |
If we apply the adjoint operator after the forward operator
as follows:
| 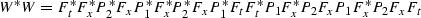 |
(59) |
with 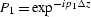 and
and 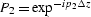 ,where P1 is a unitary operator, but P2 is a pseudo-unitary operator
because we substitute for the evanescent component when
p2 becomes imaginary.
If I group the operators so that they are in the same domain,
for example the
,where P1 is a unitary operator, but P2 is a pseudo-unitary operator
because we substitute for the evanescent component when
p2 becomes imaginary.
If I group the operators so that they are in the same domain,
for example the  domain, we get the following:
domain, we get the following:
| 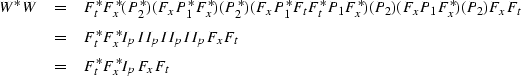 |
|
| |
| (60) |
where I is the identity matrix and Ip is an idempotent matrix
with some elements that are 1 and others that are zeros.
Therefore, the split-step Fourier extrapolation is pseudo-unitary.





Next: Datuming by wavefield depth
Up: Unitarity of the depth
Previous: Unitarity of the depth
Stanford Exploration Project
2/5/2001
![]() domain
followed by an additional phase shifting
in the
domain
followed by an additional phase shifting
in the ![]() domain.
domain.