




Next: NORMAL MOVEOUT
Up: DESIGNING PULL OPERATORS
Previous: Discretizing the output space
Generally, whatever weight is chosen for the forward operator, is also
applied to the adjoint. However, because we have changed the way we
design our operator, we must rethink our weighting. We can derive
the proper weighting function
for our Kirchoff and moveout operators in a continuum and apply it to our
operator (see Jedlicka (1989)). This means that our approximate pull adjoint is an exact
adjoint in a continuum.
We can think of a single trace of data 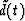 , a model trace
, a model trace
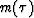 , scalar weights w and
, scalar weights w and 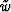 ,and an operator which performs the change of variables (this
could be NMO, for example):
,and an operator which performs the change of variables (this
could be NMO, for example):
| 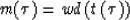 |
(1) |
| 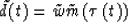 |
(2) |
We can multiply the two equations and integrate both sides with respect to
model variable  :
:
| ![\begin{displaymath}
\int m\tilde{m} \, d\tau = \int [\frac{w}{\tilde{w}} ] d\tilde{d} \, d\tau \end{displaymath}](img7.gif) |
(3) |
and change the variable of integration:
| ![\begin{displaymath}
\int m\tilde{m} \, d\tau = \int [\frac{w}{\tilde{w}} \frac{d\tau }{dt} ] d\tilde{d} \, dt\end{displaymath}](img8.gif) |
(4) |
The statement of the dot product test in a continuum is
| 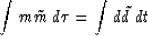 |
(5) |
which means that
| 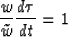 |
(6) |
From our NMO and Kirchoff equations,
| 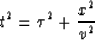 |
(7) |
| 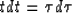 |
(8) |
| 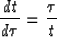 |
(9) |
This tells us the ratio of one weighting function to the other.
However, some experimentation may be required to find the optimal
choices. I find good results using w = z/t, 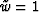 ,
but there may be more
effective combinations.
,
but there may be more
effective combinations.





Next: NORMAL MOVEOUT
Up: DESIGNING PULL OPERATORS
Previous: Discretizing the output space
Stanford Exploration Project
11/12/1997
![]() , a model trace
, a model trace
![]() , scalar weights w and
, scalar weights w and ![]() ,and an operator which performs the change of variables (this
could be NMO, for example):
,and an operator which performs the change of variables (this
could be NMO, for example):