| |
(2) |
| |
(3) |
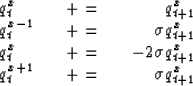 |
(4) |
Below is a Ratfor subroutine that transforms between qt and qt+1, denoted by qq() and rr(). (Unfortunately Ratfor does not admit the += notation.)
subroutine heatstep( adj, add, sigma, qq,nx, rr )
integer adj, add, nx, x
real sigma, qq(nx), rr(nx)
call adjnull( adj, add, qq,nx, rr,nx)
do x= 2, nx-1 {
if( adj == 0) {
rr(x) = rr(x) + qq(x) + ( qq(x-1) - 2*qq(x) + qq(x+1)) * sigma
} else {
qq(x ) = qq(x) + rr(x)
qq(x-1) = qq(x-1) + rr(x) * sigma
qq(x ) = qq(x ) - rr(x) * sigma * 2
qq(x+1) = qq(x+1) + rr(x) * sigma
}
}
return; end
Let us think about the adjoint calculation.
It says we can consider in turn
each temperature value qt+1x.
From this value we augment (or diminish)
neighboring temperatures according to the adjoint prescription.
Strangely, for constant ![]() and far from boundaries,
this adjoint process is equivalent to the usual
heat flow process itself (but backwards in time).
The reason it is equivalent is that each process, forward and adjoint,
is the same matrix multiplication, the forward grouped by rows
and the adjoint grouped by columns.
and far from boundaries,
this adjoint process is equivalent to the usual
heat flow process itself (but backwards in time).
The reason it is equivalent is that each process, forward and adjoint,
is the same matrix multiplication, the forward grouped by rows
and the adjoint grouped by columns.