




Next: About this document ...
Up: Harlan: Flexible tomography
Previous: REFERENCES
Assume that anisotropic velocities have a vertical axis of symmetry,
like the transversely isotropic (TI) media described in
Thomsen 1986. Although that paper describes
``weak'' anisotropy, the same equations
can be applied to very strong anisotropy Tsvankin and Thomsen (1994).
Three of Thomsen's parameters, Vz, 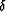 , and
, and  ,are defined by the elastic constants of a general TI medium.
These constants can be used to specify three different
effective velocities at a single point in the model.
Vz is the velocity of a wave traveling vertically along
the axis of symmetry. The velocity in any horizontal direction
is Vx determined by
,are defined by the elastic constants of a general TI medium.
These constants can be used to specify three different
effective velocities at a single point in the model.
Vz is the velocity of a wave traveling vertically along
the axis of symmetry. The velocity in any horizontal direction
is Vx determined by
| 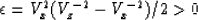 |
(19) |
and a ``normal moveout velocity'' (NMO) velocity Vn defined by
| 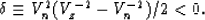 |
(20) |
Phil Anno of Conoco has shown that if
the TI properties represent the equivalent medium of
many isotropic layers Backus (1962); Schoenberg and Muir (1989),
then the above inequalities can
be expected to hold. (One additional assumption is
that the Vs/Vp ratio and Vs have a positive correlation.)
Notice that
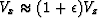 and
and
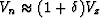 , so that
, so that 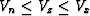 .
.
For convenience, researchers at the Colorado School of Mines
Alkhalifah and Tsvankin (1994); Tsvankin and Thomsen (1994) have also defined a constant
| 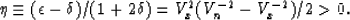 |
(21) |
Many combinations of three of these parameters can be used to describe
a TI medium. An approximation has already dropped a fourth constant
to which compressional P waves are very insensitive.
The exact equations for TI phase velocity as a function of
angle are rather clumsy, and no explicit form is available
for group velocity. Alternative approximate equations can
used which fit almost the same family of curves
as the original correct equations Michelena et al. (1993).
I use an approximate equation for group velocity
which appears to emulate closely the exact curves for
large ranges of positive  and negative
and negative 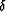 .Since I aim to estimate these anisotropic velocities from
noisy measurements, I expect our estimated curves to have larger errors
than introduced by these approximations.
.Since I aim to estimate these anisotropic velocities from
noisy measurements, I expect our estimated curves to have larger errors
than introduced by these approximations.
I choose approximate curves with the three velocities defined above.
Let 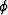 be the group angle of a raypath from the vertical.
Then the group velocity
be the group angle of a raypath from the vertical.
Then the group velocity 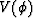 can be expressed as
can be expressed as
| 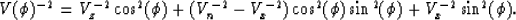 |
(22) |
Greg Lazear of Conoco found that
a good approximation of the phase velocity 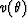 as a function of the phase angle
as a function of the phase angle 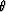 takes a similar form, but with reciprocals of velocities:
takes a similar form, but with reciprocals of velocities:
| 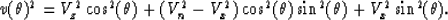 |
(23) |
The NMO velocity also turns out to have a physical
interpretation. Imagine an experiment on a homogeneous
and anisotropic medium (or imagine a small scale experiment
on a smooth model). Measure the traveltime t0 between two
points placed on a vertical line, separated by a vertical
distance Vz t0. Now displace the
upper point a distance h along a horizontal line
and measure the new traveltime th.
Then according to equation (22) the traveltime th
as a function of offset h is exactly
| ![\begin{displaymath}
t_h^2 = t_0^2 +
\left [ V_n^{-2} + (V_x^{-2} - V_n^{-2}) { h^2 \over {h^2 + V_z^2 t_0^2}}
\right ] h^2 .\end{displaymath}](img69.gif) |
(24) |
When 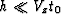 then the value of th in this
``moveout equation'' is
controlled by the NMO velocity Vn rather than Vx. In
the other case
then the value of th in this
``moveout equation'' is
controlled by the NMO velocity Vn rather than Vx. In
the other case 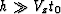 , the raypath is almost horizontal
and Vx dominates.
, the raypath is almost horizontal
and Vx dominates.
I find it convenient to define a stacking velocity Vh(h)
as a function of the offset h for a fixed vertical distance:
| 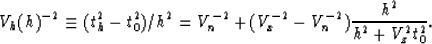 |
(25) |
Thus, we can construct a equation which describes
the best fitting hyperbola to traveltimes at zero offset
and at a single finite offset h:
|
t2 = t02 + h2 / Vh(h)2 .
|
(26) |
Note that this stacking velocity covers the range
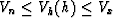 , increasing in value as h increases.
(To use two-way reflection times in 26
we need only replace the half offset
h by the full offset.)
, increasing in value as h increases.
(To use two-way reflection times in 26
we need only replace the half offset
h by the full offset.)
Theoretically, three measurements of traveltimes at three
different offsets h should uniquely determine the three
velocity constants Vz, Vx, Vn. However, the
traveltimes are much more sensitive to Vn, which determines
moveouts at small offsets, and to Vx, which determines
moveout at larger offsets. The vertical velocity Vz affects
only the rate at which the stacking velocity changes from
one limit to the other. As long as Vz has roughly the
correct magnitude, then we can fit all measured traveltimes
very well. Remember that we expect
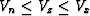 for equivalent layered media.
for equivalent layered media.
For imaging data in time, we can set Vz = Vn and simplify
our equations even further. To image surface data in depth,
we can focus images very well with good values for Vx and Vn,
then adjust imaged depths to tie wells with Vz, holding
the other two velocities constant.
Stacking velocity analysis can be optimized with Vn because
it is relatively close to Vh.
If the maximum offset equals the depth, and if Vx = 1.1 Vn,
then Vh = 1.02 Vn for a flat reflection, which is small
enough difference for such a large anisotropy.
This anisotropy model, although certainly not the most general,
describes the most important properties of transversely
isotropic velocities. The
very simple form allows for easy optimization and inversion.
A tomographic algorithm which builds on such a model will
include the necessary dependence of velocities on angle. Any
refinements in the anisotropic behavior will be easy to introduce
without major alterations of the computer program.





Next: About this document ...
Up: Harlan: Flexible tomography
Previous: REFERENCES
Stanford Exploration Project
11/12/1997
![]() , and
, and ![]() ,are defined by the elastic constants of a general TI medium.
These constants can be used to specify three different
effective velocities at a single point in the model.
Vz is the velocity of a wave traveling vertically along
the axis of symmetry. The velocity in any horizontal direction
is Vx determined by
,are defined by the elastic constants of a general TI medium.
These constants can be used to specify three different
effective velocities at a single point in the model.
Vz is the velocity of a wave traveling vertically along
the axis of symmetry. The velocity in any horizontal direction
is Vx determined by
![]() be the group angle of a raypath from the vertical.
Then the group velocity
be the group angle of a raypath from the vertical.
Then the group velocity ![]() can be expressed as
can be expressed as
![]() for equivalent layered media.
for equivalent layered media.