




Next: REFERENCES
Up: LEAST-SQUARES SEPARATION OF SIGNAL
Previous: Discussion
Conclusions
This thesis covers two methods of separating signal and noise
using multidimensional filters.
The first method is simple multidimensional filtering.
The second is using multidimensional filters to characterize the
signal and noise in an inversion process.
As a preparation for the application of these two methods,
a data editing step to remove high-amplitude noise from
the data is presented in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This removal of the worst noise improves the calculation
of the filter for simple multidimensional filtering
and prevents the noise from overwhelming the inversion
when using filters to characterize the signal and noise.
The muted data may also be predicted later during the inversion for
signal and noise.
.
This removal of the worst noise improves the calculation
of the filter for simple multidimensional filtering
and prevents the noise from overwhelming the inversion
when using filters to characterize the signal and noise.
The muted data may also be predicted later during the inversion for
signal and noise.
Filters can be designed to characterize the signal or noise
they predict by either changing the filter shape
or by limiting the data the filter is designed from to that data
dominated by either the signal or the noise.
An example of modifying the filter shape is seen
in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where the filters used for predicting
laterally continuous signals are purely lateral filters,
since predictions within a trace do not necessarily apply to
nearby traces.
Another example of a filter shaped to predict a characteristic noise
is seen in chapter
, where the filters used for predicting
laterally continuous signals are purely lateral filters,
since predictions within a trace do not necessarily apply to
nearby traces.
Another example of a filter shaped to predict a characteristic noise
is seen in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where ground roll is predicted using a filter with a large gap
to avoid predicting reflections.
,
where ground roll is predicted using a filter with a large gap
to avoid predicting reflections.
Although other methods may be used,
the filters in this thesis were
almost always calculated using a conjugate-gradient
routine.
This method simplifies and generalizes the filter calculation process,
since the conjugate-gradient technique only requires the filtering
process and its adjoint, the cross-correlation, to be specified.
Filters with dimensions higher than one are easily calculated
without the need to build the autocorrelation matrices for
the higher dimensional filters.
For the signal and noise separation by simple filtering,
I demonstrated in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) that the f-x prediction
technique of Canales 1984 and
Gulunay 1986 is equivalent to
t-x prediction using a purely lateral filter with a very long time-length.
This long time-length allowed more random noise to be passed into the
signal section; it also allowed spurious events to be generated far
from the original reflection signals.
that the f-x prediction
technique of Canales 1984 and
Gulunay 1986 is equivalent to
t-x prediction using a purely lateral filter with a very long time-length.
This long time-length allowed more random noise to be passed into the
signal section; it also allowed spurious events to be generated far
from the original reflection signals.
For both t-x and f-x prediction on three-dimensional data,
three-dimensional prediction was best done with a three-dimensional
filtering process.
Two passes of two-dimensional prediction tended to smooth out details
that were preserved with the three-dimensional prediction
filtering process.
Simple filtering to separate signal and noise has several shortcomings.
The most serious is the generation of spurious events.
While the spurious events generated by f-x prediction are
more obvious since they are well separated in time,
even the t-x prediction generates spurious events,
although these spurious events are constrained to be local.
These often appear as distortions in the wavelet of reflections.
In both f-x and t-x predictions,
spurious events are caused by the corruption of the
filter used to predict the signal by noise in the data from which the filter
is predicted.
This corruption also reduces the amplitude of reflection events,
since they are imperfectly predicted.
By recalculating a filter from an estimate of the signal obtained
from a previous pass of the inversion, an improved filter is obtained.
This improved filter may then be used to obtain a better separation
of the signal and noise.
Even with a perfect filter,
simple prediction-error filtering does not produce the desired
separation of signal and noise.
This is because
a perfectly predictable signal  removed with a
signal-annihilation filter
removed with a
signal-annihilation filter 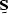 so that
so that 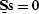 gives
gives 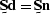 ,
not the assumed prediction-error filtering result
of
,
not the assumed prediction-error filtering result
of 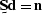 .In short, the response of the noise to the filter is left in the
signal calculated by prediction filtering.
The inversion eliminates this response of the noise to the filter
from the calculated signal.
For low amplitude noise, the response of the noise
to the filter will be small enough to ignore,
but for high amplitude noise, this response will be significant.
.In short, the response of the noise to the filter is left in the
signal calculated by prediction filtering.
The inversion eliminates this response of the noise to the filter
from the calculated signal.
For low amplitude noise, the response of the noise
to the filter will be small enough to ignore,
but for high amplitude noise, this response will be significant.
The random noise removal problem described in
chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) as a
simple prediction-error filtering process
can be changed to an effective inversion process
by using the prediction-error filter result as a starting point and
a stabilizer for the inversion, as shown in chapter
as a
simple prediction-error filtering process
can be changed to an effective inversion process
by using the prediction-error filter result as a starting point and
a stabilizer for the inversion, as shown in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Using the prediction-error filter result as an initial guess for the
inversion significantly reduces the number of iterations needed
by the inversion routine,
thus making the process only moderately more expensive than
prediction-error filtering.
Using the prediction-error filter result as a stabilization also keeps
noise out of the signal section when the signal is not perfectly
predicted by an imperfect signal-annihilation filter.
.
Using the prediction-error filter result as an initial guess for the
inversion significantly reduces the number of iterations needed
by the inversion routine,
thus making the process only moderately more expensive than
prediction-error filtering.
Using the prediction-error filter result as a stabilization also keeps
noise out of the signal section when the signal is not perfectly
predicted by an imperfect signal-annihilation filter.
The inversion process of the previous paragraph may be extended
to allow for missing data, as shown in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This is a useful feature, since bad samples that have amplitudes high enough
to spoil the least-squares inversion process may be removed
from the data as show in chapter
.
This is a useful feature, since bad samples that have amplitudes high enough
to spoil the least-squares inversion process may be removed
from the data as show in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and then recovered by the inversion.
Also, unrecorded data may be predicted by the inversion.
Prestack data tends to have more problems with both high-amplitude
bad samples and unrecorded data than the poststack data these
techniques are generally applied to.
The inversion allows random noise removal to be extended to these
prestack cases that were previously unsuited to prediction-error filtering
methods.
and then recovered by the inversion.
Also, unrecorded data may be predicted by the inversion.
Prestack data tends to have more problems with both high-amplitude
bad samples and unrecorded data than the poststack data these
techniques are generally applied to.
The inversion allows random noise removal to be extended to these
prestack cases that were previously unsuited to prediction-error filtering
methods.
Finally, when both the signal and the noise can be characterized by filters,
inversions can be set up to take advantage of the predictability.
Chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) describe some applications
of such inversions.
Perhaps the most impressive application is that of the removal
of coherent noise such as ground roll, as shown in chapter
describe some applications
of such inversions.
Perhaps the most impressive application is that of the removal
of coherent noise such as ground roll, as shown in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The techniques described in this thesis are not limited
to the problems addressed here.
In particular, the problem of multiple attenuation might be
attacked using these techniquesTaner et al. (1995).
The methods demonstrated here may also be extended from the
two- and three-dimensional forms shown here to three-, four-, or
five-dimensional applications corresponding to three-dimensional
seismic acquisition with either simple inline acquisition or
with full three-dimensional prestack geometries.
In general, these extensions are simply a matter of extending
the convolution routines to higher dimensions.
Although
the cost of higher-dimensional processing
increases with the number of dimensions,
and the amount of data recorded in some direction may not
be sufficient to allow useful predictions,
increasing the dimensionality of the predictions allows more data
to be used and better predictions to be made.





Next: REFERENCES
Up: LEAST-SQUARES SEPARATION OF SIGNAL
Previous: Discussion
Stanford Exploration Project
2/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This removal of the worst noise improves the calculation
of the filter for simple multidimensional filtering
and prevents the noise from overwhelming the inversion
when using filters to characterize the signal and noise.
The muted data may also be predicted later during the inversion for
signal and noise.
.
This removal of the worst noise improves the calculation
of the filter for simple multidimensional filtering
and prevents the noise from overwhelming the inversion
when using filters to characterize the signal and noise.
The muted data may also be predicted later during the inversion for
signal and noise.