




Next: Methods of using a
Up: The calculation of a
Previous: The calculation of a
While measures of the residuals other than the L-2 norm
may be used,
the least-squares method is used here.
Norms between one and two may be obtained with the iteratively
re-weighted least-squares (IRLS)
methodDarche (1989); Green (1984); Nichols (1994b).
Norms other than L-2, especially L-1, may be used in cases where
the presence of high-amplitude events overwhelm the least-squares
residuals.
In this thesis, two different approaches to high-amplitude errors are taken.
In chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the problem of high-amplitude noise corrupting the filter
calculation is solved by iteratively solving for a signal and
a signal annihilation filter.
Another approach is taken in chapter
,
the problem of high-amplitude noise corrupting the filter
calculation is solved by iteratively solving for a signal and
a signal annihilation filter.
Another approach is taken in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where samples that produce large residuals are removed before the inversion,
then, in chapter
,
where samples that produce large residuals are removed before the inversion,
then, in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the signal and noise are separated simultaneously with the
prediction of the missing data caused by the sample removal.
It is hoped that these techniques will solve most practical problems.
,
the signal and noise are separated simultaneously with the
prediction of the missing data caused by the sample removal.
It is hoped that these techniques will solve most practical problems.
The calculation of a filter is done by solving 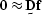 ,where
,where 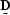 is a matrix made up of the given data
and
is a matrix made up of the given data
and 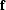 is the filter to be solved for.
Claerbout1992a shows how to solve for
this filter
is the filter to be solved for.
Claerbout1992a shows how to solve for
this filter 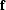 by expressing the convolution of the filter
by expressing the convolution of the filter 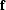 and
the data
and
the data 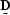 as matrix operators and their adjoints.
If the operator and its adjoint are available, a conjugate-gradient
routine may be used to calculate a least-squares minimization
of a systemLuenburger (1984).
This approach to computing the filter simplifies the problem considerably.
Two- and three-dimensional filters may be calculated as simply as
a one-dimensional filter, provided the filter operation and its adjoint
are available.
as matrix operators and their adjoints.
If the operator and its adjoint are available, a conjugate-gradient
routine may be used to calculate a least-squares minimization
of a systemLuenburger (1984).
This approach to computing the filter simplifies the problem considerably.
Two- and three-dimensional filters may be calculated as simply as
a one-dimensional filter, provided the filter operation and its adjoint
are available.





Next: Methods of using a
Up: The calculation of a
Previous: The calculation of a
Stanford Exploration Project
2/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the problem of high-amplitude noise corrupting the filter
calculation is solved by iteratively solving for a signal and
a signal annihilation filter.
Another approach is taken in chapter
,
the problem of high-amplitude noise corrupting the filter
calculation is solved by iteratively solving for a signal and
a signal annihilation filter.
Another approach is taken in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where samples that produce large residuals are removed before the inversion,
then, in chapter
,
where samples that produce large residuals are removed before the inversion,
then, in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the signal and noise are separated simultaneously with the
prediction of the missing data caused by the sample removal.
It is hoped that these techniques will solve most practical problems.
,
the signal and noise are separated simultaneously with the
prediction of the missing data caused by the sample removal.
It is hoped that these techniques will solve most practical problems.