In geophysical filtering applications,
the matrix ![]() is often, although not always,
Toeplitz.
(A Toeplitz matrix is a matrix in which each row is a shifted version
of the others and has constant diagonals).
In general,
if the type of filter application is transient convolution,
convolution with the data sequence padded with zeros,
is often, although not always,
Toeplitz.
(A Toeplitz matrix is a matrix in which each row is a shifted version
of the others and has constant diagonals).
In general,
if the type of filter application is transient convolution,
convolution with the data sequence padded with zeros,
![]() is Toeplitz,
but if the filter application is internal
(unpadded convolution)
or truncated-transient (transient convolution truncated to the input length),
is Toeplitz,
but if the filter application is internal
(unpadded convolution)
or truncated-transient (transient convolution truncated to the input length),
![]() is no longer in a Toeplitz formClaerbout (1995).
When
is no longer in a Toeplitz formClaerbout (1995).
When ![]() is Toeplitz, the matrix can be
represented by a single row of the matrix, since a Toeplitz
matrix is made up of a single row shifted so that a particular element is
always on the diagonal.
This makes the matrix easy to store in a computer memory,
and easy to solve, since an efficient algorithm for solving Toeplitz systems,
that of Levinson recursion, existsKanasewich (1981).
is Toeplitz, the matrix can be
represented by a single row of the matrix, since a Toeplitz
matrix is made up of a single row shifted so that a particular element is
always on the diagonal.
This makes the matrix easy to store in a computer memory,
and easy to solve, since an efficient algorithm for solving Toeplitz systems,
that of Levinson recursion, existsKanasewich (1981).
In the cases where ![]() is not Toeplitz,
it is still symmetric, and this symmetry can be useful
in calculating
is not Toeplitz,
it is still symmetric, and this symmetry can be useful
in calculating ![]() .Another useful feature of
.Another useful feature of ![]() is
that it is generally positive definite.
Although
is
that it is generally positive definite.
Although ![]() is guaranteed to only be positive semidefinite,
in practice a small stabilizer
is guaranteed to only be positive semidefinite,
in practice a small stabilizer ![]() is added to
is added to ![]() to force it to be positive definite.
The idea of adding
to force it to be positive definite.
The idea of adding ![]() can be viewed as forcing
all the eigenvalues to be greater than
can be viewed as forcing
all the eigenvalues to be greater than ![]() and eliminating any zero eigenvalues.
That
and eliminating any zero eigenvalues.
That ![]() is positive definite
can be seen from the definition of a positive definite matrix,
where
is positive definite
can be seen from the definition of a positive definite matrix,
where ![]() is positive definite if
is positive definite if
![]() is always positiveStrang (1986).
If
is always positiveStrang (1986).
If ![]() and
and ![]() is full rank,
then
is full rank,
then ![]() ,
which is always positive for non-zero
,
which is always positive for non-zero ![]() .Since
.Since ![]() is positive definite,
it can be solved by Cholesky factorizationStrang (1988).
Cholesky factorization allows
a positive definite matrix
is positive definite,
it can be solved by Cholesky factorizationStrang (1988).
Cholesky factorization allows
a positive definite matrix ![]() to be factored as
to be factored as ![]() , where
, where
![]() is a lower triangular matrix and
is a lower triangular matrix and ![]() is the corresponding
upper triangular matrix.
The cost of solving a system with Cholesky factorization
is about half that of a general linear system solver,
and the method is generally accurate (Makhoul 1975 in
Childers 1978).
Efficient methods for Cholesky factorization to solve
such systems are given in LINPACKDongarra et al. (1979)
and in Tarantola 1987.
is the corresponding
upper triangular matrix.
The cost of solving a system with Cholesky factorization
is about half that of a general linear system solver,
and the method is generally accurate (Makhoul 1975 in
Childers 1978).
Efficient methods for Cholesky factorization to solve
such systems are given in LINPACKDongarra et al. (1979)
and in Tarantola 1987.
For a Toeplitz matrix, the storage requirements are small,
since only one row of the matrix needs to be stored.
In the more general case, where ![]() is symmetric positive definite,
half the matrix needs to be stored for Cholesky factorization.
When the inversion requires a fairly small matrix
is symmetric positive definite,
half the matrix needs to be stored for Cholesky factorization.
When the inversion requires a fairly small matrix ![]() ,Levinson recursion or Cholesky factorization methods are sufficient.
Later in this thesis, larger problems than those that can be practically solved
with these methods will be addressed,
but it can be seen that even for filter calculations,
these computations may become difficult because of their size.
For example, when calculating a one-dimensional filter,
the number of elements in the matrix
,Levinson recursion or Cholesky factorization methods are sufficient.
Later in this thesis, larger problems than those that can be practically solved
with these methods will be addressed,
but it can be seen that even for filter calculations,
these computations may become difficult because of their size.
For example, when calculating a one-dimensional filter,
the number of elements in the matrix ![]() is required
to be the
square of the number of elements in the filter.
If the type of filter application is transient convolution,
only one column of
is required
to be the
square of the number of elements in the filter.
If the type of filter application is transient convolution,
only one column of ![]() needs to be stored,
but if the filter application is internal or truncated-transient convolution,
needs to be stored,
but if the filter application is internal or truncated-transient convolution,
![]() is no longer Toeplitz and half of the
elements in the matrix need to be stored.
For a short one-dimensional filter, this is generally a reasonable requirement.
is no longer Toeplitz and half of the
elements in the matrix need to be stored.
For a short one-dimensional filter, this is generally a reasonable requirement.
For two- or three-dimensional filters,
the filters could be calculated by getting the inverse of ![]() ,but the size of this matrix will tend to be very large.
Consider, for example, a small two-dimensional problem, where the
filter is
,but the size of this matrix will tend to be very large.
Consider, for example, a small two-dimensional problem, where the
filter is
| (22) |
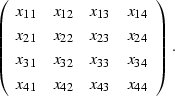 |
(23) |
 |
(24) |
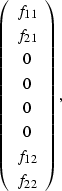 |
(25) |
In addition to the large size of the ![]() matrix,
multi-dimensional filters tend to have many more coefficients
than one-dimensional filters
because of the higher number of dimensions involved.
This increases the cost of solving for the filter by either the
square or the cube of the number of coefficients,
depending on the solution method.
When internal convolutions with
multi-dimensional filters
are desired,
matrix,
multi-dimensional filters tend to have many more coefficients
than one-dimensional filters
because of the higher number of dimensions involved.
This increases the cost of solving for the filter by either the
square or the cube of the number of coefficients,
depending on the solution method.
When internal convolutions with
multi-dimensional filters
are desired,
![]() is no longer Toeplitz,
and half of the huge
is no longer Toeplitz,
and half of the huge ![]() matrix must be stored and solved.
matrix must be stored and solved.
When inversions need to be done to predict
full seismic datasets rather than just small filters,
the number of elements to be calculated may be in the thousands or
millions, making the number of elements in the matrix ![]() in the millions or billions.
Solving, or even storing, such large matrices will generally be impractical.
in the millions or billions.
Solving, or even storing, such large matrices will generally be impractical.
Later I will discuss the conjugate-gradient technique,
which allows an iterative solution to these inversion problems.
The conjugate-gradient technique has the advantage that
the matrix ![]() does not need to be stored,
and a good approximation to the
answer may be had by limiting the number of iterations,
thus reducing the cost.
Also, the programming of the problem tends to be simpler, since the
conjugate-gradient technique requires just the coding of the
convolution and its
conjugate-transpose, or adjoint.
does not need to be stored,
and a good approximation to the
answer may be had by limiting the number of iterations,
thus reducing the cost.
Also, the programming of the problem tends to be simpler, since the
conjugate-gradient technique requires just the coding of the
convolution and its
conjugate-transpose, or adjoint.