

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Amplitude preserving offset continuation
in theory
Part 1: The offset continuation equation
Sergey Fomel
sergey@sep.stanford.edu
ABSTRACT
This paper concerns amplitude-preserving kinematically equivalent
offset continuation (OC) operators. I introduce a revised partial
differential OC equation as a tool to build
OC operators that preserve offset-dependent reflectivity in prestack
processing. The method of characteristics is applied to reveal the
geometric laws of the OC process. With the help of geometric
(kinematic) constructions, the equation is proved to be
kinematically valid for all
offsets and reflector dips in constant velocity media.
In the OC process,
the angle-dependent reflection coefficient is preserved, and the
geometric spreading factor is transformed in accordance with the laws
of geometric seismics independently of the reflector curvature.
|
Offset continuation (OC) by definition is an operator that transforms
common-offset seismic gathers from one constant offset to another
(). Bagaini et al.
recently identified OC with a whole family of prestack
continuation operators, such as shot continuation
(, ), dip moveout as a particular case of OC
to zero offset, and three-dimensional azimuth moveout
(). Possible practical applications of OC
operators include regularizing seismic data by partial stacking
prior to prestack migration () and
interpolating missing data. Since dip moveout (DMO) represents a particular
case of offset continuation to zero offset, the OC concept is also
one of the possible approaches to DMO. Another
prospective application of prestack continuation operators, pointed
out recently by Fabio Rocca (personal communication), is prestack
tomography-type velocity analysis.
In the theory of OC operators, two issues need to be addressed. The first
is kinematic equivalence. We expect seismic sections
obtained by OC to contain correctly positioned reflection
traveltime curves. The second issue is amplitude equivalence.
If the traveltimes are positioned correctly, it is wave
amplitudes that deserve most of our attention. Since the final outputs
of the seismic processing sequence are the
migrated sections, the kinematic equivalence of OC concerns
preserving the true geometry of seismic images, while the amplitude
equivalence addresses preserving the desired brightness of the images.
Apparently, there can be different definitions of
amplitude-preserving or true-amplitude processing. The most
commonly used one (, , , )
refers to the reflectivity preservation. According to this
definition, amplitude-preserving seismic data processing should make
the image amplitudes proportional to the reflection coefficients that
correspond to the initial constant-offset gathers. This point of view
implies that an amplitude-preserving OC operator tends to transform
offset-dependent amplitude factors, except for the reflection coefficient,
in accordance with the geometric seismic laws.
In this paper I introduce a theoretical approach to constructing
different types of OC operators with respect to both kinematic equivalence and
amplitude preservation.
The first part presents the theory for a revised OC
differential equation. As early as in 1982, Bolondi et al.
came up with the idea of describing OC as a
continuous process
by means of a partial differential equation ().
However, their approximate differential OC operator,
built on the results of Deregowski and Rocca's classic paper
,
turned out to fail in case of steep reflector dips or large offsets.
In his famous Ph.D. thesis Dave Hale wrote:
The differences between this algorithm [DMO by Fourier
transform] and previously published finite-difference DMO algorithms
are analogous to the differences between frequency-wavenumber
(, ) and finite-difference
() algorithms for migration. For example,
just as finite-difference migration algorithms require approximations
that break down at steep dips, finite-difference DMO algorithms are
inaccurate for large offsets and steep dips, even for constant velocity.
Continuing this analogy, one can observe that both
finite-difference and frequency-domain migration algorithms share
a common origin: the wave equation. The new OC equation, presented in
this paper and valid for all
offsets and
dips,
can play an analogous role for offset continuation and dip moveout
algorithms. The next section
begins with a rigorous proof
of the revised equation's kinematic validity. Since the OC process belongs
to the wave type, it is appropriate to describe it by
considering wavefronts (which in this case correspond to the traveltime
curves) and ray trajectories (referred to in this paper as time
rays). The laws of amplitude transport along the time rays illuminate the main
dynamic properties of offset continuation and prove the OC equation's
amplitude equivalence.
INTRODUCING THE OFFSET CONTINUATION EQUATION
Most of the contents of this paper refer to the following linear
partial differential equation:
| 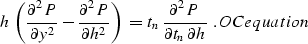 |
(1) |
Equation OCequation describes an imaginary (nonphysical)
process of reflection seismic data transformation in the
offset-midpoint-time domain. Here h stands for the half-offset
(h=(r-s)/2, where s and r are the source and the receiver
coordinates), y is the midpoint (y=(r+s)/2), and tn is the time
coordinate after normal moveout correction is applied
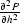 .The velocity v is supposed to be constant and known a priori.
.The velocity v is supposed to be constant and known a priori.
Equation OCequation and the previously
published OC equation () differ
only with respect to the
single term  . However, this
difference is substantial. As Appendix A proves, the
range of validity for the approximate OC equation
. However, this
difference is substantial. As Appendix A proves, the
range of validity for the approximate OC equation
| 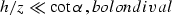 |
(2) |
can be defined by the inequality
| 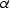 |
(3) |
where z is the reflector depth, and  is the dip angle. For example,
for a dip of 45 degrees, equation bolondi is valid only for
offsets that are much smaller than the depth.
is the dip angle. For example,
for a dip of 45 degrees, equation bolondi is valid only for
offsets that are much smaller than the depth.
In order to prove the theoretical validity of equation OCequation for
all offsets and reflector dips, I apply a simplified version of the
ray method technique (, ) and obtain two equations to
describe separately wavefront (traveltime) and amplitude
transformation in the OC process. According to the formal ray theory, the
leading term of the high-frequency asymptotics for a reflected wave,
recorded on a seismogram, takes the form
| 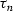 |
(4) |
where An stands for the amplitude, Rn is the wavelet shape of the
leading high-frequency term, and  is the traveltime curve
after normal moveout. Inserting raymethod as a trial
solution for OCequation, collecting terms that have the same
asymptotic order, and neglecting low-order terms produces a set of
two first-order partial differential equations:
is the traveltime curve
after normal moveout. Inserting raymethod as a trial
solution for OCequation, collecting terms that have the same
asymptotic order, and neglecting low-order terms produces a set of
two first-order partial differential equations:
| 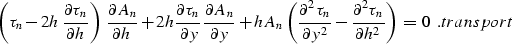 |
(5) |
| 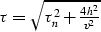 |
(6) |
Equation eikonal describes the transformation of traveltime
curve geometry in the OC process analogously to the eikonal
equation in the wavefront propagation theory. Thus, what appear to be
wavefronts of the wave
motion described by OCequation are traveltime
curves of reflected waves recorded on seismic sections.
The law of amplitude transformation for high-frequency wave components,
related to those wavefronts, is given by transport.
In terms of the theory
of partial differential equations, equation eikonal is
the characteristic equation for OCequation.
Proof of kinematic equivalence
In order to prove the validity of equation eikonal, it is
convenient to transform it
to the coordinates of the initial shot gathers: s=y-h, r=y+h, and
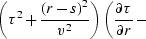 . The transformed equation takes the
form
. The transformed equation takes the
form
| 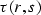 |
(7) |
Now the goal is to prove that any reflection traveltime function
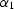 in a constant velocity medium satisfies equation SCeikonal.
in a constant velocity medium satisfies equation SCeikonal.
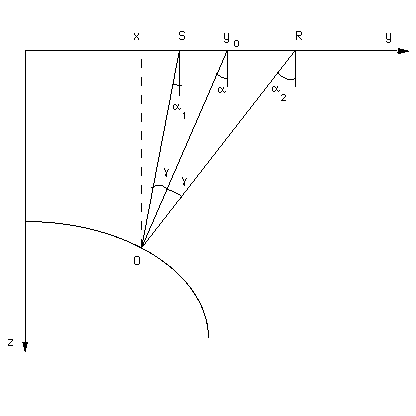
Let S and R be the source and the reflection locations, and O be
a reflection point for that pair.
Note that the incident ray SO and the reflected ray
OR form a triangle with the basis on the offset SR (l=|SR|=r-s).
Let
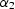 be the angle of SO from the vertical axis, and
be the angle of SO from the vertical axis, and  be the
analogous angle of RO (Figure ocoray). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
be the
analogous angle of RO (Figure ocoray). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
| 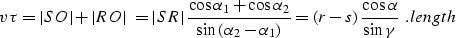 |
(8) |
| (9) |
Hence, the total length of the reflected ray is
| 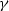 |
(10) |
Here 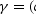 is the reflection angle (
is the reflection angle (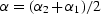 ), and
), and  is the central ray angle (
is the central ray angle (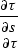 ) coincident with the local dip angle of the reflector at
the reflection point.
Recalling the well-known relationships between the ray angles and the
first-order traveltime derivatives
) coincident with the local dip angle of the reflector at
the reflection point.
Recalling the well-known relationships between the ray angles and the
first-order traveltime derivatives
| 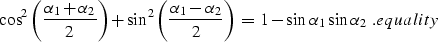 |
(11) |
| (12) |
we can substitute length, snell1, and snell2 into
SCeikonal, which leads to the simple trigonometric equality
| 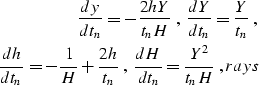 |
(13) |
It is now easy to prove that equality equality is true for any
 and
and  .
.
ocoray
Figure 1 Reflection rays in a constant
velocity medium (a scheme).
|
|  |

Thus we have proved that equation
SCeikonal, equivalent to eikonal, is valid in constant
velocity media independently of the reflector geometry and the offset.
This means that high-frequency asymptotic components of the waves,
described by the OC equation,
are located on the true reflection traveltime curves.
The theory of characteristics can provide other ways to prove the kinematic
validity of equation eikonal, as described in (, ).
Offset continuation geometry: time rays
To study the laws of traveltime curve transformation in
the OC process, it is convenient to apply the method of
characteristics () to the eikonal-type equation eikonal. The
characteristics of eikonal (bi-characteristics with respect to
OCequation) are the trajectories of the high-frequency energy
propagation in the imaginary OC process. Following the formal analogy
with seismic rays, let's call those trajectories time rays, where
the word time refers to the fact that time rays describe
the traveltime transformation.
According to the theory of first-order partial differential equations,
time rays are determined by a set of ordinary
differential equations (characteristic equations) derived from
eikonal :
| 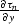 |
|
| (14) |
where Y corresponds to 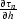 along a ray, and H corresponds to
along a ray, and H corresponds to  . In this coordinate system, equation eikonal takes the form
. In this coordinate system, equation eikonal takes the form
| 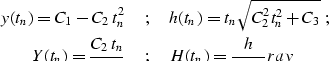 |
(15) |
and serves as an additional constraint for the definition of time rays.
System rays can be solved by standard mathematical methods. Its
general solution takes the parametric form, where the time
variable tn is the parameter along a time ray:
| 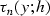 |
(16) |
| (17) |
and C1, C2, and C3 are independent coefficients, constant along each
time ray. To determine the values of these coefficients, we can
pose an initial value
(Cauchy) problem for the system of differential equations rays.
The traveltime curve  for a given common offset h and
the first partial derivative
for a given common offset h and
the first partial derivative  along
the same constant offset section provide natural initial conditions for
the Cauchy problem. A particular case of those conditions is the
zero-offset traveltime curve. If the first partial derivative
of traveltime with respect to offset is continuous, it vanishes at
zero offset according to
the reciprocity principle (traveltime must be an even function
of the offset):
along
the same constant offset section provide natural initial conditions for
the Cauchy problem. A particular case of those conditions is the
zero-offset traveltime curve. If the first partial derivative
of traveltime with respect to offset is continuous, it vanishes at
zero offset according to
the reciprocity principle (traveltime must be an even function
of the offset):
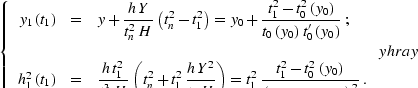 Applying the initial value conditions to the general solution ray
generates the following expressions for the ray invariants:
Applying the initial value conditions to the general solution ray
generates the following expressions for the ray invariants:
| 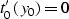 |
|
| (18) |
Finally, substituting abc into ray produces an explicit
parametric form of
the ray trajectories:
| 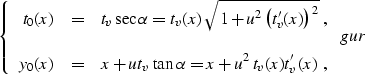 |
(19) |
Here y1, h1, and t1 are the coordinates of the continued seismic
section. The first of equations yhray indicates that the time
ray projections to a common-offset section
have a parabolic form. Time rays don't exist for  (a locally horizontal reflector), because in this case
post-NMO offset continuation
transform is not required.
(a locally horizontal reflector), because in this case
post-NMO offset continuation
transform is not required.
The actual parameter that
determines a particular time ray is the reflection point location.
This important conclusion follows from the known parametric equations
| 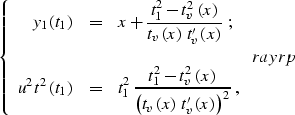 |
(20) |
where x is the reflection point, u is half of the wave velocity (u=v/2),
tv is the vertical time (reflector depth divided by u), and
 is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
| 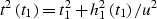 |
(21) |
and substituting gur into yhray, we get
| 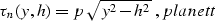 |
(22) |
where 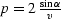 .
.
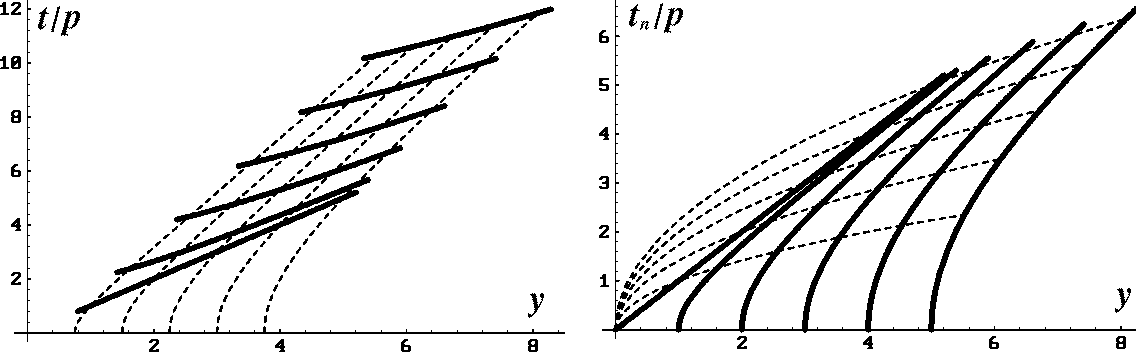
To visualize the concept of time rays, let's consider some simple analytic
examples of its application to geometric analysis of
the offset continuation process.
The
simplest and most important example is the case of a plane dipping
reflector. Putting
the origin of the y axis at the reflector plane intersection with the
surface, we can express the reflection traveltime after NMO in the form
| 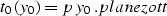 |
(23) |
where 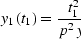 , and
, and  is the dip angle.
The zero-offset traveltime in this case is a straight line:
is the dip angle.
The zero-offset traveltime in this case is a straight line:
| 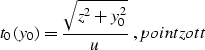 |
(24) |
According to yhray, time rays are defined by
| 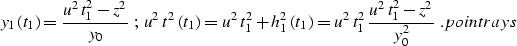 |
(25) |
The geometry of the OC transformation is shown in Figure
ocopln.
ocopln
Figure 2 Transformation of
the reflection traveltime curves in the OC process: the case of a plane dipping
reflector. Left: Time coordinate before the NMO correction. Right:
Time coordinate after NMO. Solid lines indicate traveltime curves;
dashed lines, time rays.

The second example is the case of a point diffractor (the left side of Figure
ococrv).
Without loss of generality, the origin of the midpoint axis can be put
above the
diffraction point. In this case
the zero-offset reflection traveltime curve has the well-known
hyperbolic form
| 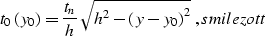 |
(26) |
where z is the depth of the diffractor, and u=v/2 is half of the wave
velocity. Time rays are defined according to yhray,
as follows:
| 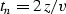 |
(27) |
ococrv
Figure 3 Transformation of
the reflection traveltime curves in the OC process. Left: the case of
a diffraction point.
Right: the case of an elliptic reflector. Solid lines indicate traveltime
curves; dashed lines, time rays.

The third curious example (the right side of Figure ococrv) is the case
of a focusing
elliptic reflector. Let y be the center of the ellipse
and h be half the distance between the focuses of the ellipse. If both
focuses are on the surface, the zero-offset traveltime curve is defined by the
so-called ``DMO smile'' ():
| 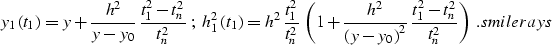 |
(28) |
where 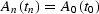 , and z is the small semi-axis of the ellipse.
The time ray equations are
, and z is the small semi-axis of the ellipse.
The time ray equations are
| 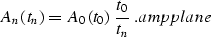 |
(29) |
When y1 coincides with y, and h1 coincides with h, the source and the
receiver are in the focuses of the elliptic reflector, and the traveltime curve
degenerates to a point t1=tn. This remarkable fact is the actual
basis of the
geometric theory of dip moveout ().
Proof of amplitude equivalence
This section discusses the connection between the laws of traveltime
transformation and the laws of the corresponding amplitude transformation.
The change of the wave amplitudes in the OC process is described by
the first-order partial differential transport equation transport. The
general solution of this equation can be found by applying
the method of
characteristics. It takes the
explicit integral form
| 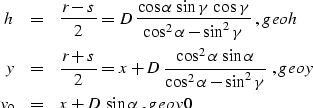 |
(30) |
The integral in ampint is defined on a curved time ray, and An(tn)
stands for the amplitude transported along this ray. In the case of a plane
dipping reflector, the ray amplitude can be immediately evaluated by
substituting the explicit traveltime and time ray formulas from the
preceding section into ampint. The amplitude expression in
this case takes the simple form
| 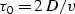 |
(31) |
In order to consider the more general case of a curvilinear reflector,
we need to
take into account a connection between the traveltime
derivatives in ampint and the geometric quantities of the reflector.
As follows directly from the trigonometry of the incident and reflected rays
triangle (Figure ocoray),
| 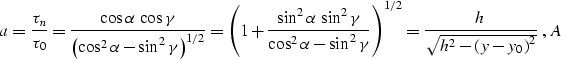 |
(32) |
| (33) |
| (34) |
where D is the length of the normal ray. Let 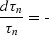 be the
zero-offset reflection traveltime. Combining geoh and geoy0 with
length we can get the following relationship:
be the
zero-offset reflection traveltime. Combining geoh and geoy0 with
length we can get the following relationship:
| 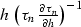 |
(35) |
which interprets the ``DMO smile'' smilezott found by Deregowski
and Rocca
in geometric terms. Equation A
allows a convenient change of variables in ampint. Let the
reflection angle 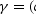 be a parameter monotonously increasing along a time
ray. In this case, each time ray is uniquely determined by the position of the
reflection point, which in turn is defined by the values of D and
be a parameter monotonously increasing along a time
ray. In this case, each time ray is uniquely determined by the position of the
reflection point, which in turn is defined by the values of D and
 . According to this change of variables we can differentiate A
along a time ray to get
. According to this change of variables we can differentiate A
along a time ray to get
| 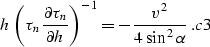 |
(36) |
Note also that the quantity 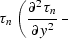 in ampint coincides exactly with the time ray invariant
C3 found in abc. Therefore its value is constant along each time ray
and equals
in ampint coincides exactly with the time ray invariant
C3 found in abc. Therefore its value is constant along each time ray
and equals
| 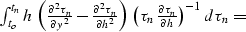 |
(37) |
Finally, as shown in Appendix B,
| 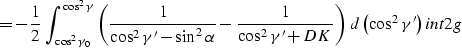 |
(38) |
where K is the reflector curvature at the reflection point. Substituting
dt2tg, c3, and curve into ampint transforms
the integral
to the form
| 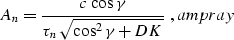 |
(39) |
which we can evaluate analytically. The final formula for the
amplitude transformation takes the form
| 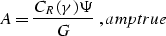 |
|
| (40) |
In case of a plane reflector, the curvature K is zero, and ampcurve
coincides with ampplane. Equation ampcurve can be rewritten as
| 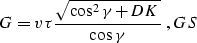 |
(41) |
where c is constant along each time ray (it may vary with the reflection point
location on the reflector but not with the offset). We should compare equation
ampray
with the known expression for the reflection wave amplitude of the leading
ray series term in 2.5-D media:
| 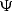 |
(42) |
where CR stands for the angle-dependent reflection coefficient, G is the
geometric spreading
| 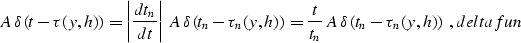 |
(43) |
and  includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
ampray coincides completely with the true geometric spreading factor
GS, and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in raymethod) is described
by the delta function, then, as follows from the known properties of
this function,
includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
ampray coincides completely with the true geometric spreading factor
GS, and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in raymethod) is described
by the delta function, then, as follows from the known properties of
this function,
| 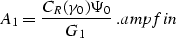 |
(44) |
which leads to the equality
| 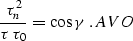 |
(45) |
Combining a2an with amptrue and ampray allows us to
evaluate the amplitude after continuation from some initial offset h0 to
another offset h1, as follows:
| 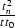 |
(46) |
Equation ampfin indicates that the OC process described by equation
OCequation is amplitude-preserving in the sense that corresponds to the
so-called Born DMO (, ). This means that
the geometric spreading factor from the initial amplitudes is transformed to
the
true geometric spreading on the continued section, while the reflection
coefficient stays the same. This remarkable dynamic property allows AVO
(amplitude versus offset) analysis to be performed by a dynamic comparison
between true constant-offset sections and the sections transformed by OC from
different offsets. With a simple trick, the offset coordinate is
transferred to the reflection
angles for the AVO analysis.
As follows from A and length,
| 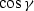 |
(47) |
If we include the 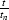 factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO
section obtained without this factor, the resultant amplitude of the reflected
events
will be directly proportional to
factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO
section obtained without this factor, the resultant amplitude of the reflected
events
will be directly proportional to 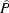 , where the reflection angle
, where the reflection angle
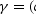 corresponds to the initial offset. Of course, this conclusion is
rigorously
valid for constant-velocity 2.5-D media only.
corresponds to the initial offset. Of course, this conclusion is
rigorously
valid for constant-velocity 2.5-D media only.
Black et al. recently suggested a definition of
true-amplitude DMO different from that of Born DMO. The difference
consists of
two important components:
- 1.
- True-amplitude DMO addresses preserving the peak amplitude of the
image wavelet instead of preserving its spectral density.
In the terms of this
paper, the peak amplitude corresponds to the initial amplitude A instead of
the spectral density amplitude An. A simple correction factor
 would help us
take the difference between the two amplitudes into account. Multiplication by
would help us
take the difference between the two amplitudes into account. Multiplication by
 can be easily done at the NMO stage.
can be easily done at the NMO stage.
- 2.
- Seismic sections are multiplied by time to correct for the geometric
spreading factor prior to DMO (or in our case, offset continuation)
processing.
As follows from GS, multiplication by t is a valid geometric
spreading correction for plane reflectors only.
It is amplitude-preserving
offset continuation based on the OC equation OCequation that
is able to correct
for the curvature-dependent factor in the amplitude. To take into account
the second aspect of Black's definition, we can consider the wave
field  such
that
such
that
| 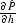 |
(48) |
Substituting p2pt into the OC equation OCequation transforms the
latter to the form
| 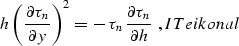 |
(49) |
Equations BSZequation and OCequation differ only with
respect to the first-order term  .This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation eikonal depends on the second-order terms only.
Offset continuation operators based on BSZequation conform to
Black's definition of true-amplitude processing.
.This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation eikonal depends on the second-order terms only.
Offset continuation operators based on BSZequation conform to
Black's definition of true-amplitude processing.
I have introduced a partial differential equation OCequation and
proved that the process described by it provides for a kinematically and
dynamically equivalent offset continuation transform. Kinematic
equivalence means that in constant velocity media the reflection
traveltimes are transformed to their true
locations on different offsets. Dynamic equivalence means that the
geometric spreading term in the amplitudes of reflected waves
transforms in accordance with the geometric seismics laws, while the
angle-dependent reflection coefficient stays the same in the OC
process. The amplitude properties of amplitude-preserving OC may find an
important application in the seismic data processing connected with AVO
interpretation .
The offset continuation equation can be applied directly to design OC
operators of the finite-difference type. Other types of operators are
related to different forms of the solutions of the OC equation.
Part 2 of this paper will describe integral-type offset continuation
operators based on the initial value problem associated with equation
OCequation. Other important topics in the theory of offset
continuation include
- Connection between OC and amplitude-preserving
frequency-domain DMO
- Connection between OC and true-amplitude prestack migration
- Generalizing the OC concept to 3-D azimuth moveout (AMO)
Sergey Goldin drew my attention to the role of curvature
dependence in reflected wave amplitudes. The last section of this paper
partially overlaps with the contents of our joint paper ().
[paper,SEP,GEOPHYSICS,EAEG,MISC,SEGCON]
A
RANGE OF VALIDITY FOR BOLONDI'S OC EQUATION
From the OC characteristic equation eikonal we can conclude that
the first-order
traveltime derivative with respect to offset decreases with a decrease
of the offset. At zero offset the derivative equals zero, as predicted by the
principle of reciprocity (reflection traveltime has to be an
even function of offset). Neglecting  in eikonal leads to the characteristic equation
in eikonal leads to the characteristic equation
| 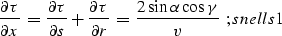 |
(50) |
which corresponds to the approximate OC equation bolondi of
Bolondi et al. . Comparing
ITeikonal and eikonal, note that approximation
ITeikonal is valid only if
| 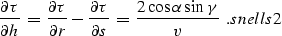 |
(51) |
To find the geometric constraints implied by inequality
condition, we can express the traveltime derivatives in
geometric terms. As follows from expressions snell1 and snell2,
| 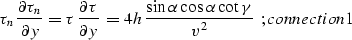 |
(52) |
| 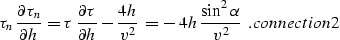 |
(53) |
Expression length allows transforming snells1 and
snells2 to the form
| 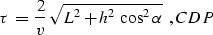 |
(54) |
| 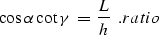 |
(55) |
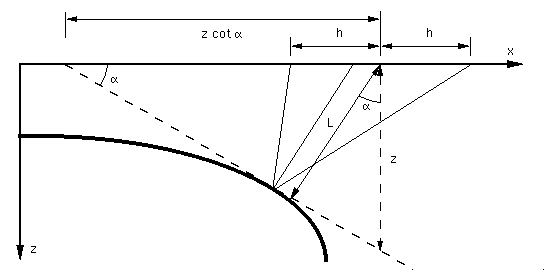
Without loss of generality, we can assume  to be positive.
Consider a plane tangent to the true reflector at the reflection
point
(Figure ocobol).
The traveltime of the wave, reflected from the plane, has the
well-known explicit expression
to be positive.
Consider a plane tangent to the true reflector at the reflection
point
(Figure ocobol).
The traveltime of the wave, reflected from the plane, has the
well-known explicit expression
| 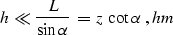 |
(56) |
where L is the length of the normal ray from the midpoint. As
follows from combining CDP and length,
| 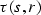 |
(57) |
We can then combine equalities ratio, connection1,
connection2
snells1, and snells2 to
transform inequality condition to the form
| 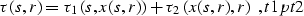 |
(58) |
where z is the depth of the plane reflector under the midpoint.
The proven inequality hm coincides with bolondival in
the main text.
ocobol
Figure 4 Reflection rays and
tangent to the reflector in a constant velocity medium (a scheme).

B
SECOND-ORDER REFLECTION TRAVELTIME DERIVATIVES
In this appendix I derive formulas connecting second-order partial
derivatives of the reflection traveltime with the geometric properties
of the reflector in a constant velocity medium. These formulas are used in the
main text of the paper for the amplitude behavior description.
Let 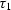 be the reflection traveltime from the source s to the
receiver r. Consider a formal equality
be the reflection traveltime from the source s to the
receiver r. Consider a formal equality
| 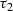 |
(59) |
where x is the reflection point parameter,  corresponds to the
incident ray, and
corresponds to the
incident ray, and  corresponds to the reflected ray.
Differentiating t1pt2 with respect to s and r yields
corresponds to the reflected ray.
Differentiating t1pt2 with respect to s and r yields
| 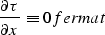 |
(60) |
| 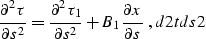 |
(61) |
According to Fermat's principle, the two-point reflection ray path must
correspond to the traveltime extremum. Therefore
| 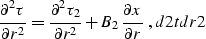 |
(62) |
for any s and r. Taking into account fermat while differentiating
dt1ds and dt2dr, we get
| 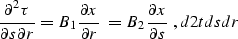 |
(63) |
| 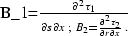 |
(64) |
| 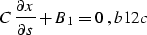 |
(65) |
where
Differentiating fermat gives us the additional pair of equations
| 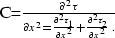 |
(66) |
| 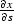 |
(67) |
where
Solving the system b12c - b22c for  and
and
 and substituting the result into d2tds2 -
d2tdsdr
produces the following set of expressions:
and substituting the result into d2tds2 -
d2tdsdr
produces the following set of expressions:
| 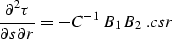 |
(68) |
| 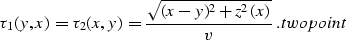 |
(69) |
| 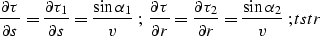 |
(70) |
In the case of a constant velocity medium, expressions cs2 to
csr can be applied directly to the explicit
formula for the two-point eikonal
| 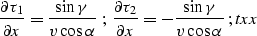 |
(71) |
Differentiating twopoint and taking into account the trigonometric
relationships for the incident and reflected rays (Figure
ocoray), one can
evaluate all the quantities in cs2 to csr explicitly.
After some heavy algebra, the resultant expressions for the traveltime
derivatives take the form
| 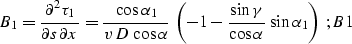 |
(72) |
| 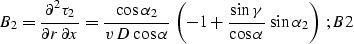 |
(73) |
| 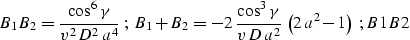 |
(74) |
| 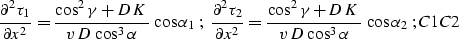 |
(75) |
| 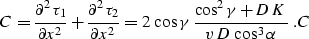 |
(76) |
| 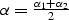 |
(77) |
| 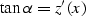 |
(78) |
Here D is the length of the normal (central) ray,  is its dip angle
(
is its dip angle
(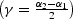 ,
, 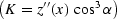 ),
),
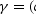 is the reflection angle
is the reflection angle
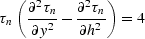 , K is the reflector
curvature at the reflection point , and
a is the nondimensional function of
, K is the reflector
curvature at the reflection point , and
a is the nondimensional function of  and
and 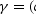 defined in A.
defined in A.
The formulas derived in this appendix were used to get the formula
which coincides with curve in the main text.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
 . However, this
difference is substantial. As Appendix A proves, the
range of validity for the approximate OC equation
. However, this
difference is substantial. As Appendix A proves, the
range of validity for the approximate OC equation
 is the dip angle. For example,
for a dip of 45 degrees, equation bolondi is valid only for
offsets that are much smaller than the depth.
is the dip angle. For example,
for a dip of 45 degrees, equation bolondi is valid only for
offsets that are much smaller than the depth.
 is the traveltime curve
after normal moveout. Inserting raymethod as a trial
solution for OCequation, collecting terms that have the same
asymptotic order, and neglecting low-order terms produces a set of
two first-order partial differential equations:
is the traveltime curve
after normal moveout. Inserting raymethod as a trial
solution for OCequation, collecting terms that have the same
asymptotic order, and neglecting low-order terms produces a set of
two first-order partial differential equations:
![]() . The transformed equation takes the
form
. The transformed equation takes the
form
![]() be the angle of SO from the vertical axis, and
be the angle of SO from the vertical axis, and  be the
analogous angle of RO (Figure ocoray). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
be the
analogous angle of RO (Figure ocoray). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
 is the central ray angle (
is the central ray angle (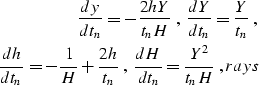
 .
.
 . In this coordinate system, equation eikonal takes the form
. In this coordinate system, equation eikonal takes the form
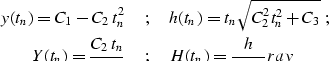
 along
the same constant offset section provide natural initial conditions for
the Cauchy problem. A particular case of those conditions is the
zero-offset traveltime curve. If the first partial derivative
of traveltime with respect to offset is continuous, it vanishes at
zero offset according to
the reciprocity principle (traveltime must be an even function
of the offset):
along
the same constant offset section provide natural initial conditions for
the Cauchy problem. A particular case of those conditions is the
zero-offset traveltime curve. If the first partial derivative
of traveltime with respect to offset is continuous, it vanishes at
zero offset according to
the reciprocity principle (traveltime must be an even function
of the offset):
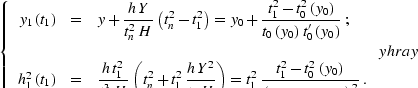 Applying the initial value conditions to the general solution ray
generates the following expressions for the ray invariants:
Applying the initial value conditions to the general solution ray
generates the following expressions for the ray invariants:
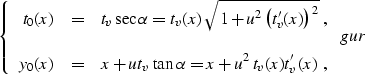
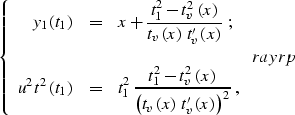
 is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
 is the dip angle.
The zero-offset traveltime in this case is a straight line:
is the dip angle.
The zero-offset traveltime in this case is a straight line:
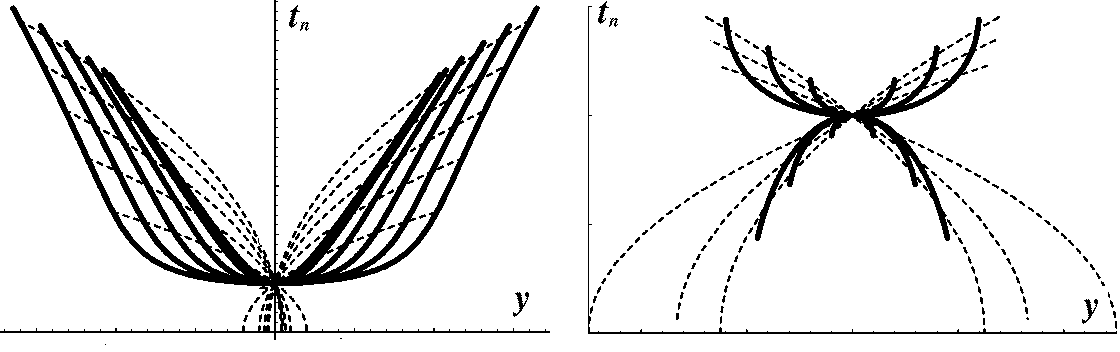
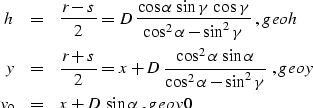
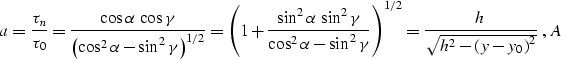
 . According to this change of variables we can differentiate A
along a time ray to get
. According to this change of variables we can differentiate A
along a time ray to get
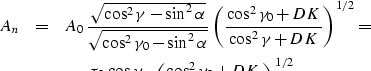
 includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
ampray coincides completely with the true geometric spreading factor
GS, and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in raymethod) is described
by the delta function, then, as follows from the known properties of
this function,
includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
ampray coincides completely with the true geometric spreading factor
GS, and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in raymethod) is described
by the delta function, then, as follows from the known properties of
this function,
 would help us
take the difference between the two amplitudes into account. Multiplication by
would help us
take the difference between the two amplitudes into account. Multiplication by
 can be easily done at the NMO stage.
can be easily done at the NMO stage.
 such
that
such
that
 .This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation eikonal depends on the second-order terms only.
Offset continuation operators based on BSZequation conform to
Black's definition of true-amplitude processing.
.This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation eikonal depends on the second-order terms only.
Offset continuation operators based on BSZequation conform to
Black's definition of true-amplitude processing.
 in eikonal leads to the characteristic equation
in eikonal leads to the characteristic equation
 to be positive.
Consider a plane tangent to the true reflector at the reflection
point
(Figure ocobol).
The traveltime of the wave, reflected from the plane, has the
well-known explicit expression
to be positive.
Consider a plane tangent to the true reflector at the reflection
point
(Figure ocobol).
The traveltime of the wave, reflected from the plane, has the
well-known explicit expression
![]() be the reflection traveltime from the source s to the
receiver r. Consider a formal equality
be the reflection traveltime from the source s to the
receiver r. Consider a formal equality
 corresponds to the
incident ray, and
corresponds to the
incident ray, and  corresponds to the reflected ray.
Differentiating t1pt2 with respect to s and r yields
corresponds to the reflected ray.
Differentiating t1pt2 with respect to s and r yields
 and
and
 and substituting the result into d2tds2 -
d2tdsdr
produces the following set of expressions:
and substituting the result into d2tds2 -
d2tdsdr
produces the following set of expressions:
 is its dip angle
(
is its dip angle
( and
and ![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)