|
ras18
Figure 1 Raw April 18 data after binning. |  |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTA multigrid nonlinear algorithm was applied to the April 18 SeaBeam data set to fill in the large regions of missing data, obtaining an image superior to those obtained with linear methods, and more quickly than is possible with a normal, single grid nonlinear interpolation. The model may be chosen to contain any number of points; here models with gradually increasing numbers of points are solved for in succession, each providing the initial guess for the next. The algorithm is unstable in some cases, but in general converges quickly to a detailed solution. |
INTRODUCTION
Figure ras18 displays a portion of a data set collected by SeaBeam, a system for recording water depth below a ship and at some distance to either side. SeaBeam data is recorded by towing sonar instruments, each transmitting a narrow beam and recording the travel time and angle of the backscattered signal. A depth is determined for each signal using this travel time, angle, and an assumed velocity for the signal in water. The data appear in sweeps, beginning at a wide angle and sweeping through vertical to another wide angle on the opposite side of the ship. The resulting data set is a track about fifteen points wide, following the course of the ship; each data point is an (x,y,z) triplet.
The data were collected over a mid-ocean ridge which is visible in the plot of the raw data. In the more sparsely sampled areas are segments of ridges which we may guess run parallel to the spreading center ridge. Intuitively we would like a missing data inversion which will connect these segments, and which will give a detailed output where data is more plentiful, as in the left portion of the survey area.
This is accomplished by nonlinear inverse interpolation. Claerbout has demonstrated its effectiveness on this data set. I combine his method with multigrid to produce results with less computational effort. In addition to being faster, the multigrid method produces a sharper image of the interpolated topography.
In this paper, I describe how inverse interpolation in general is formulated, and the multigrid method employed here. I also offer what I feel are improved final results.
|
ras18
Figure 1 Raw April 18 data after binning. |  |
|
hector
Figure 2 Closeup of SeaBeam density plot to show acquisition, prepared by Hector Urdaneta. | 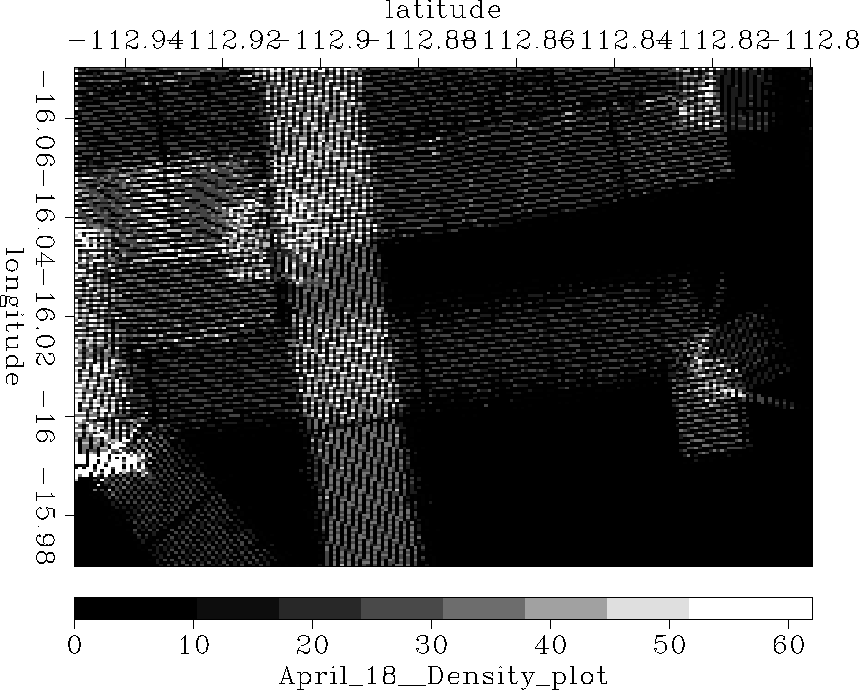 |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)