![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1] (
[1] (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
[1]
)
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1]
[1]
[1]
[1]
et al.
[1]
[1]
[1]
[1]
[1]
[1]
et al.
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) Proof:
Remark:
Proof:
Remark:
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1] (
[1] (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
[1]
)
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) [1]
[1]
[1]
[1]
[1]
et al.
[1]
[1]
[1]
[1]
[1]
[1]
et al.
[1] ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) Proof:
Remark:
Proof:
Remark:
 |
(1) |
S T V W min [1]LS[#1] [1]LS[#1] Int Bdy k_- k_+ k_s i(r - t) i(r - t) i(z - t)
ABSTRACTPractical algorithms for solving realistic inverse problems may often be viewed as problems in nonlinear programming with the data serving as constraints. Such problems are most easily analyzed when it is possible to segment the solution space into regions that are feasible (satisfying all the known constraints) and infeasible (violating some of the constraints). Then, if the feasible set is convex or at least compact, the solution to the problem will normally lie on the boundary of the feasible set. A nonlinear program may seek the solution by systematically exploring the boundary while satisfying progressively more constraints. Examples of inverse problems in wave propagation (traveltime tomography) and vibration (modal analysis) are presented to illustrate how the variational structure of these problems may be used to create nonlinear programs using implicit variational constraints. |
INTRODUCTION
Although the most common method used to analyze inverse problems is perturbation theory and/or linearization, it is generally recognized that most inverse problems of practical interest are mathematically nonlinear. The inherent nonlinearities lead to the necessity of distinguishing local minima from global minima. Optimization methods based on objective functionals typically produce ``solutions'' that minimize the functional ``locally'' -- i.e., in the vicinity of the starting point of the minimization process.
The methods discussed in the present paper have been developed specifically to improve our insight into the structure of certain classes of nonlinear inverse problems. Furthermore, once this structure is understood, methods of solution of the inverse problems using nonlinear programming methods are immediately suggested by the particular variational structure observed.
The first example presented uses vibration frequencies of a taut string to deduce its mass distribution. The pertinent variational principle for this problem is Rayleigh-Ritz. The second example uses traveltime data to deduce wave velocity using Fermat's principle of least-time. The remaining examples use frequencies of free oscillation of the Earth to deduce density and elastic parameters. The pertinent variational principle is again Rayleigh-Ritz, but significant differences in the variational structure arise between these examples and the string density vibration analysis problem. The structures possessed by members of this set of problems appears to span the range of possible variational structures and provides some new insights into potential inversion algorithms for some of the problems.
STRING VIBRATION ANALYSIS
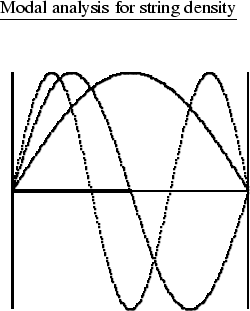 |
The equation of vibration for a simple string is
^2 ut^2 =
T ^2 ux^2,
where t is the time, x is the spatial coordinate of the string along its
length, ![]() is the density distribution of the string,
T is the tension in the string (assumed constant), and u(x,t) is the normal
displacement of the string from its equilibrium position as a function
of both position and time. The ends of the string are fixed, so
the boundary conditions are u(0,t) = 0 = u(1,t). I assume
that the string's temporal motion may be decomposed into its Fourier
components so that I may study standing waves on the plucked string.
The time dependence is assumed to separate out in one of the forms
is the density distribution of the string,
T is the tension in the string (assumed constant), and u(x,t) is the normal
displacement of the string from its equilibrium position as a function
of both position and time. The ends of the string are fixed, so
the boundary conditions are u(0,t) = 0 = u(1,t). I assume
that the string's temporal motion may be decomposed into its Fourier
components so that I may study standing waves on the plucked string.
The time dependence is assumed to separate out in one of the forms
![]() ,
, ![]() , or
, or ![]() , where
, where ![]() is
angular frequency with dimensions of radians/sec, while f is frequency in
Hz. Then, the equation (waveeqn) reduces to
is
angular frequency with dimensions of radians/sec, while f is frequency in
Hz. Then, the equation (waveeqn) reduces to
-^2u = T u_xx,
where I have now introduced the subscript notation
for derivatives such that
![]() ,
, ![]() , etc.
, etc.
I assume that the tension T in the string is known, but the density
distribution ![]() of the string is unknown. Our goal is to determine to
what extent
of the string is unknown. Our goal is to determine to
what extent ![]() can be determined using knowledge of modes of
vibration of the string. In particular, I assume that some measurements
of the vibration frequencies for standing waves have been made.
can be determined using knowledge of modes of
vibration of the string. In particular, I assume that some measurements
of the vibration frequencies for standing waves have been made.
Let ![]() be the eigenfrequency and un(x) the eigenfunction of the
n-th Fourier component for
be the eigenfrequency and un(x) the eigenfunction of the
n-th Fourier component for ![]() . Higher n corresponds to
eigenfunctions with more internal nodes, e.g.,
n=1 has no internal nodes, n=2 has one internal node, etc.
Then, after choosing unit tension T=1, I multiply (waveeqn2) by
un(x) and integrate along the length of the string to show that
. Higher n corresponds to
eigenfunctions with more internal nodes, e.g.,
n=1 has no internal nodes, n=2 has one internal node, etc.
Then, after choosing unit tension T=1, I multiply (waveeqn2) by
un(x) and integrate along the length of the string to show that
_n^2() = _0^1 u_n,x^2(x)dx_0^1 (x)u_n^2(x)dx.
To arrive at (eigenfrequencyident),
I integrated once by parts (![]() )using the fact that un(0) = 0 = un(1) to eliminate the boundary
contribution. Equation (eigenfrequencyident) is an identity satisfied
by the n-th eigenfrequency and relating it to the integrated properties of
the n-th eigenfunction.
)using the fact that un(0) = 0 = un(1) to eliminate the boundary
contribution. Equation (eigenfrequencyident) is an identity satisfied
by the n-th eigenfrequency and relating it to the integrated properties of
the n-th eigenfunction.
Now the Rayleigh-Ritz method for characterizing eigenvalues [Courant and Hilbert, 1953] may be applied to the string problem and it shows that
_1^2() [,v_1]
_0^1 v_1,x^2(x)dx_0^1 (x)v_1^2(x)dx,
where is the Rayleigh-Ritz quotient with
v1(x) being any trial function satisfying the boundary conditions
v1(0) = 0 = v1(1) whose first derivative with respect to x
is finite everywhere along the interval containing the string. When
the string density distribution ![]() is known,
the Rayleigh-Ritz method may be used as a numerical method for
finding estimates of both the eigenfrequency
is known,
the Rayleigh-Ritz method may be used as a numerical method for
finding estimates of both the eigenfrequency ![]() and the eigenfunction
u1(x); the theory shows that
and the eigenfunction
u1(x); the theory shows that ![]() if and only if v1(x) = u1(x) almost everywhere.
Similarly, if I impose constraints on the trial function such as requiring
vn(x) to have n-1 interior nodes [Coddington and Levinson, 1955],
then (RR1) generalizes to
if and only if v1(x) = u1(x) almost everywhere.
Similarly, if I impose constraints on the trial function such as requiring
vn(x) to have n-1 interior nodes [Coddington and Levinson, 1955],
then (RR1) generalizes to
_n^2() [,v_n]
_0^1 v_n,x^2(x)dx_0^1 (x)v_n^2(x)dx.
The characteristic frequencies (the ![]() s) are those defined in
(eigenfrequencyident) for the higher order modes.
I will sometimes refer to the equations (RR1) and (RRn)
as the ``forward problem,'' since in these equations I assume that the density
distribution is a known quantity. The ``inverse problem'' is the harder
problem of taking measured values of the eigenfrequencies
s) are those defined in
(eigenfrequencyident) for the higher order modes.
I will sometimes refer to the equations (RR1) and (RRn)
as the ``forward problem,'' since in these equations I assume that the density
distribution is a known quantity. The ``inverse problem'' is the harder
problem of taking measured values of the eigenfrequencies ![]() and
attempting to solve for the
unknown density distribution
and
attempting to solve for the
unknown density distribution ![]() .
.
Feasibility analysis
There are two tricks that make it possible in some cases to use the variational functionals to analyze inversion problems. The first trick is a result of what I call the ``scale invariance'' property of the eigenfunctions in certain problems. For a given density distribution and its corresponding eigenfunction u(x), the only effect of multiplying by a constant is to change the eigenfrequency by the factor . This result follows since
[,u] = [,u]/, which implies that I conclude that each eigenfunction u(x) is determined only by the relative variations in the density, not by the absolute scale.
The second trick is a result of the linear dependence of the denominator of the Rayleigh-Ritz functional on the density distribution . I take advantage of this linearity in with greater ease by working with the reciprocal of , so I first note that
1[,v] = (x)v^2(x)dxv_x^2(x)dx ^-2(). Now, if I have made measurements of some of the eigenfrequencies of the string, I can ask the following question: Are there density distributions that violate the inequality in (inversecalR)? That is, if I try to compute the left hand side of (inversecalR) using an arbitrary trial density distribution , when will the inequality be satisfied and when will it be violated? I use the answers to these questions to define two distinct classes of trial model density distributions :
If 1[,v_n] _n^2() for each measured frequency _n, then (x) is feasible. However,
if 1[,v_n] > _n^2() for any measured frequency _n, then (x) is infeasible.
As defined here, the concepts of feasible and infeasible
trial density distributions depend explicitly on the available data ![]() and implicitly on the trial functions
vn(x). However, it is also possible to show [Berryman, 1991]
that universal (global)
feasible and infeasible sets exist that are independent of the particular trial
functions chosen (dependence on the particular choice of the subset of those
measured frequencies which are used in the analysis still remains).
The concepts of feasible
and infeasible sets are commonly found in texts on nonlinear programming
methods [Fiacco and McCormick, 1990]. Since the method I develop
for solving the inverse problem
is a type of nonlinear programming method, it is not surprising that
these concepts also arise in the context of numerical methods for
solving inverse problems.
and implicitly on the trial functions
vn(x). However, it is also possible to show [Berryman, 1991]
that universal (global)
feasible and infeasible sets exist that are independent of the particular trial
functions chosen (dependence on the particular choice of the subset of those
measured frequencies which are used in the analysis still remains).
The concepts of feasible
and infeasible sets are commonly found in texts on nonlinear programming
methods [Fiacco and McCormick, 1990]. Since the method I develop
for solving the inverse problem
is a type of nonlinear programming method, it is not surprising that
these concepts also arise in the context of numerical methods for
solving inverse problems.
Now, I derive a very useful property of the class of feasible density distributions. Consider some trial eigenfunction v(x) and two feasible trial densities and ,which therefore (by assumption) satisfy
1[_a,v] ^-2() and 1[_b,v] ^-2(). Let be a number in the range . Then, taking a linear combination of the two expressions in (feasibletrials) gives
[_a,v] + 1-[_b,v] ^-2(). But, the left hand side of (convexcombination) may be rewritten as
[_a(x)+(1-)_b(x)]v^2(x)dx v_x^2(x)dx = 1[_,v], where I have defined the convex combination of the trial densities to be
_(x) _a(x)+(1-)_b(x). Combining (convexcombination) and (combination) shows that
1[_,v] ^-2(). But any trial function that satisfies the analog of (convexity) for all frequencies considered from the measurement set is by definition feasible. So, if and are both feasible, their convex combination is also feasible.
The definition of a convex set is this: a set such that the convex combination -- e.g., -- of any two members is also a member of the set. So, this fact implies that the set of all feasible density distributions for a given set of vibration data (and a given set of trial eigenfunctions) is a convex set. In general, convex sets are very useful in computations because they are often compact and always have smooth boundaries.
Now, the first trick (scale invariance) plays an interesting and important role in the analysis. Suppose I have any trial density distribution and I have found the eigenfunctions un(x) and eigenvalues associated with this distribution. Then, the eigenfunctions un(x) are also the eigenfunctions for all densities of the form ,where is an arbitrary positive scalar. It is not hard to show [Berryman, 1991] that there always exists a choice of such that lies exactly on the boundary of the feasible set for the inversion problem. It follows then that, if ,the density lies in the feasible part of the model space; while, if , the density lies in the infeasible part. This characteristic of the feasible set allows us to produce a simple geometrical interpretation of the feasible set.
In particular, for the vibrating string inversion problem, the feasible set of model densities is compact and occupies a convex region in the neighborhood of the origin of the model space [i.e., near ]. I easily prove this statement. First note that a mass density must be nonnegative, so the physical model space is the convex set (actually a cone) of all possible nonnegative density distributions. Then, by taking the trial eigenfunction to be with the trial density (constant), and noting that
1[_0,v_1] = _0^2xdx ^2^2xdx = _0^2 satisfies the feasibility constraint if
_0 ^2_1^-2().
The first measured eigenfrequency ![]() then determines an upper bound on
the value of for
constant density models. For nonconstant models such as the two component
string with for and
for , the same argument shows that
then determines an upper bound on
the value of for
constant density models. For nonconstant models such as the two component
string with for and
for , the same argument shows that
1[,v_1] = _a_0^12 ^2xdx +_b_12^1 ^2xdx^2_0^1 ^2x dx = _a+_b2^2 _1^-2(). Thus, (tauabound) show that is bounded above by the straight line
_b 2^2_1^-2() - _a, producing tighter bounds on as increases. When , this problem reduces to the constant model result found earlier. These simple examples can be used to produce further restrictions on model densities.
Although the analysis presented is fine for the lowest eigenfrequency,
complications arise for the higher frequencies ![]() , for all .For these higher eigenfrequencies, the Rayleigh-Ritz functional
requires some constraints on the trial eigenfunctions (i.e., for
, for all .For these higher eigenfrequencies, the Rayleigh-Ritz functional
requires some constraints on the trial eigenfunctions (i.e., for
![]() , the trial function vn should be orthogonal to the eigenfunctions
um for m < n). These restrictions on the eigenfunctions guarantee
the existence of correlations between the model and the trial eigenfunctions
that would be neglected if we tried to make direct use of the preceding
analysis for the higher order eigenfunctions. I will show what the
consequences of these correlations are when I present the general analysis of
variational structure for inverse problems later in the paper. The main
result will be that a feasible set for the Rayleigh-Ritz variational problem
still exists, but it can be nonconvex when the variational functionals become
nonlinear as they do when such correlations arise.
, the trial function vn should be orthogonal to the eigenfunctions
um for m < n). These restrictions on the eigenfunctions guarantee
the existence of correlations between the model and the trial eigenfunctions
that would be neglected if we tried to make direct use of the preceding
analysis for the higher order eigenfunctions. I will show what the
consequences of these correlations are when I present the general analysis of
variational structure for inverse problems later in the paper. The main
result will be that a feasible set for the Rayleigh-Ritz variational problem
still exists, but it can be nonconvex when the variational functionals become
nonlinear as they do when such correlations arise.
Algorithm
Now I describe a general algorithm for solving the inverse problem for a two-segment string. This algorithm involves a lot of forward modeling, but will always produce a good approximation to the solution. First, note that the symmetry of the problem guarantees that if solves the problem then so does . (I am presently considering only the frequencies as data. This nonuniqueness of the solution can be easily removed by considering the eigenfunctions as data as well.) Thus, I only need to consider half of the positive quadrant, say for models such that . Then, picking models evenly spaced in angle for (say) 10 angles up to , so with .(The precise value of does not matter, since these points will eventually be scaled onto the feasibility boundary.) Having chosen a set of initial points, I now do forward modeling on each of these string models. After scaling to the feasibility boundary, I check satisfaction of the data and pick the two adjacent points that best satisfy the data. Then, I divide the angular region bracketed by these two angles into 10 smaller angles, and repeat this process until I have a satisfactory solution. The algorithm just described is basically a ``shooting'' algorithm for the inverse problem.
The algorithm just described is probably overly complex for the two component string problem. It is not hard to show that the two lowest frequencies are enough to determine the densities of the two segments (although not enough to tell which is which) when it is known that the segments are of equal length. For such a simple problem, other algorithms that are more efficient could be devised to make optimal use of this information. The real advantage of the approach becomes more apparent when we consider more complex models involving three or more string segments. The inversion algorithm just described is easily generalized to many segments of constant density and the resulting algorithm is complicated only by the need to define an efficient means of choosing points in the model space for each forward modeling phase of the calculation. It is also clear that algorithms of this type can easily be parallelized, with an individual processor assigned to do a single forward modeling computation at each step of the algorithm.
TRAVELTIME INVERSION PROBLEM
A typical problem arising in seismic traveltime inversion in 2- and 3-dimensional heterogeneous media is the need to infer the (isotropic) compressional-wave slowness (reciprocal of velocity) distribution of a medium, given a set of observed first-arrival traveltimes between sources and receivers of known location within the medium [Dines and Lytle, 1979; Lytle and Dines, 1980]. This problem is common for crosswell seismic transmission tomography imaging a 2-D region occupying the plane between two vertical boreholes in oil field applications. I could also consider the problem of inverting for wave slowness when the absolute traveltimes are not known perfectly, as is normally the case in earthquake seismology for whole Earth structure [Aki and Richards, 1980].
Wave slowness models
When a sound wave or seismic wave is launched into a medium, it takes time for the influence of the wave to progress from a point close to the source to a more distant point. The time taken by the wave to travel from one point of interest to the next is called the traveltime. The local slowness is the inverse of the local wave speed. It is most convenient to develop inversion and tomography formulas in terms of wave slowness models, because the pertinent equations are linear in slowness.
I might consider three kinds of slowness models. I allow the slowness to be a general function of the position . However, I often make one of two more restrictive assumptions that (i) the model comprises homogeneous cells (in 2-D), or blocks (in 3-D), with sj then denoting the slowness value of the jth cell, or block. Or (ii) the model is defined in terms of a grid with values of slowness assigned at the grid points together with some interpolation scheme (bilinear, trilinear, spline, etc.) to specify the values between grid points. Of course, as cells/blocks become smaller and smaller (down to infinitesimal), I think of cells/blocks of constant slowness as a special case of continuous models, or of continuous models as a limiting case of cells/blocks.
When it is not important which type of slowness model is involved, I refer to the model abstractly as a vector in a vector space . For a block model with n blocks, I have , the n-dimensional Euclidean vector space. A continuous slowness model, on the other hand, is an element of a function space, e.g., the set of continuous functions of three real variables. No matter how I parameterize the model, these models necessarily have far fewer parameters than the actual medium they are intended to represent. Thus, these models are analogous to cartoons, trying to capture the main features with the minimum of detail.
Fermat's principle and traveltime functionals
The traveltime of a seismic wave is the integral of slowness along a ray path connecting the source and receiver. To make this more precise, I define two types of functionals for traveltime.
Let P denote an arbitrary path connecting a given source and receiver in a slowness model . I will refer to P as a trial ray path. I define a functional , which yields the traveltime along path P. Letting be the continuous slowness distribution , I have
^P[] = _P s()dl^P, where dlP denotes the infinitesimal distance along the path P.
Fermat's principle states that the correct ray path between two points is the one of least overall traveltime, i.e., it minimizes with respect to path P.
Let us define a second traveltime functional to be the functional that yields the traveltime along the Fermat (least-time) ray path. Fermat's principle then states
^*[] = _PPaths ^P[], where Paths denotes the set of all continuous paths connecting the given source and receiver. The particular path that produces the minimum in (b) is denoted P*. If more than one path produces the same minimum traveltime value, then P* denotes any particular member in this set of minimizing paths.
Substituting (a) into (b), I have Fermat's principle of least time:
^*[]=_P^* s()dl^P^*=_P _P s()dl.^P The traveltime functional is well-known to be stationary with respect to small variations in the path P*(s).
Seismic inversion and tomography
Suppose I have a set of observed traveltimes, t1, ..., tm, from m source-receiver pairs in a medium of slowness . Let Pi be the Fermat ray path connecting the ith source-receiver pair. Neglecting observational errors, I write
_P_i s()dl^P_i = t_i, i=1,...,m.
Given a block slowness model, let lij be the length of the ith ray path through the jth cell:
l_ij = _P_icell_jdl^P_i. For n cells, Eq.(tta) can then be written
_j=1^n l_ij s_j = t_i, i=1,...,m. Note that for any given i, the ray-path lengths lij are zero for most cells j, as a given ray path will in general intersect only a few of the cells in the model.
I rewrite (ttb) in matrix notation by defining the column vectors and and the matrix as follows: Equation (ttb) then becomes the basic equation of forward modeling for ray equation analysis:
= . Note that equation (ttc) may be viewed as a numerical approximation to equation (d), i.e., it is just a discretized (or finite element) version of the equation. Equation (ttc) may be used for any set of ray paths, whether those ray paths minimize (d) or not. If the ray paths used to form the matrix are actually minimizing ray paths, is then implicitly a function of the slowness model .
The methods developed apply to both two-dimensional and three-dimensional imaging applications.
Feasibility analysis for traveltime inversion The idea of using feasibility constraints in nonlinear programming problems is well established [Fiacco and McCormick, 1990]. However, comparatively little attention has been given to the fact that physical principles such as Fermat's principle actually lead to rigorous feasibility constraints for nonlinear inversion problems [Berryman, 1991]. The main practical difference between the standard analysis in nonlinear programming and the analysis being developed for nonlinear inversion is that, whereas the functions involved in nonlinear programming are often continuous, differentiable, and relatively easy to compute explicitly, the functionals in nonlinear inversion (e.g., the traveltime functional) need not be continuous or differentiable and, furthermore, are very often rather difficult to compute. Feasibility constraints for such inversion problems are generally implicit, rather than explicit.
Equation (tta) assumes that Pi is one of Fermat's (least-time) paths and leads to the equalities summarized in the vector-matrix equation . Now suppose instead that Pi is a trial ray path which may or may not be a least-time path. Fermat's principle allows us to write
_P_i s()dl^P_i t_i, where now ti is the measured traveltime for source-receiver pair i. When I discretize (fca) for cell or block models and all ray paths i, the resulting set of m inequalities may be written as
Equations (fca) and (fcb) can be interpreted as a set of inequality constraints on the slowness model . When obeys these m constraints, I say that is feasible. When any of the constraints is violated, I say is infeasible. The set of inequalities collectively are called the feasibility constraints.
The concept of the feasibility constraint is quite straightforward in nonlinear programming problems [Fiacco and McCormick, 1990] whenever the constraints may be explicitly stated for the solution vector. However, in these inversion problems, an additional computation is required. The feasibility constraints are explicit for the traveltime data vector, but they are only implicit (i.e., they must be computed) for the slowness vector. This added degree of complication is unavoidable in the inversion problem, but nevertheless it is also very easily handled computationally with only very minor modifications of the usual nonlinear inversion algorithms.
Now suppose are two model vectors in the feasible set for a given set of ray paths . Let be the convex combination of these two vectors, where .Since, for each fixed ray path i, the traveltime functional is a linear functional of the slowness model, I have
_i^P(_) = _i^P(_1) + (1-) _i^P(_2).
But (by assumption) and and are non-negative. Therefore,
_i^P(_) t_i + (1-) t_i = t_i.
Thus, the convex combination lies in the feasible set if and do, so it follows again that the feasible set for the traveltime time problem is convex. This shows that for a fixed set of ray paths the local feasibility set is convex.
One important difference between the traveltime inversion problem and the string density inversion problem is that whereas the hierarchy of variational functionals used in the Rayleigh-Ritz approach contains inherent nonlinearities due to the necessity of orthogonalizing higher order trial eigenfunctions with respect to lower order ones, no such necessity arises in the traveltime problem. Each traveltime measurement is in a very real sense independent of every other traveltime measurement; all traveltimes are equally important and no hierarchy of traveltimes needs to be established. Although it is certainly possible to use trial ray paths that are highly correlated with the wave speed models under consideration, such correlations are not required by Fermat's principle in the way that they are by the Rayleigh-Ritz method. (For example, we could do the entire tomographic inversion using straight rays, with some loss of accuracy in the final result.) This fact suggests, but does not prove, that the global feasible set for the traveltime problem is itself convex. Using the fact that the global feasible set must be the intersection of all possible feasible sets, we obtain a proof of convexity [Berryman, 1991].
Algorithms
Stable reconstruction algorithms using feasibility constraints to solve the traveltime tomography problem have been discussed in detail elsewhere [Berryman, 1990]. The key idea is to use the fact that the solution, if one exists, must lie on the feasibility boundary and then to force the solution in an iterative scheme to stay close to this manifold in the model space. An iterative linear least-squares inversion algorithm was easily and cheaply stablized using this approach. Other choices of algorithms based on the feasibility constraints are also possible, as will be discussed at the end of the paper.
CONSTRAINTS FOR EARTH DENSITY DISTRIBUTION
A somewhat different class of problems involves analysis of free oscillations of the Earth in order to deduce its density structure [MacDonald and Ness, 1961; Gilbert, 1971; Jordan and Anderson, 1974; Aki and Richards, 1980; Gilbert, 1980; Ben-Menahem and Singh, 1981; Lapwood and Usami, 1981; Morelli and Dziewonski, 1987; Snieder, 1993]. I concentrate on toroidal modes since they are independent of gravitational effects.
For each normal mode of a vibrating elastic medium, the potential energy density is composed of a bulk contribution proportional to the bulk modulus and a shear contribution proportional to the shear modulus. B and S are functionals of the exciting eigenfunctions. If the compressional and shear wave speeds (vc and vs, respectively) have been found using (for example) traveltime tomography, then I use the identities
v_s^2 = /, with being the mass density, to show that the potential energy density may be written in the form
U = [(v_c^2-4 v_s^2/3) B + v_s^2 S]. This equation shows explicitly that the potential energy is the sum of terms proportional to the unknown density, the squares of the (assumed) known velocities, and the functionals B and S of the (possibly trial) eigenfunctions.
The kinetic energy of a vibrating system is proportional to the
density and the square of the time rate of change of the local displacement;
so the Fourier transform of this energy density takes the general form
, where ![]() is the angular frequency of oscillation,
and K is the square of the trial displacement.
is the angular frequency of oscillation,
and K is the square of the trial displacement.
The partitioning of energy in a vibrating medium is known to balance the total kinetic and potential energy in the volume over a cycle. If the volume is , this balance between the two energies may be expressed in the equality
^2_ K d= _ U d,
where again is the local density, K and U are functionals of the
eigenfunctions of the normal modes of vibration, and ![]() is the
angular frequency of vibration for a particular mode. It is
well-known that equation (energyeqn) can be rewritten in the form
of a variational inequality as
is the
angular frequency of vibration for a particular mode. It is
well-known that equation (energyeqn) can be rewritten in the form
of a variational inequality as
^2 U dK d, in which the right hand side is again the Rayleigh-Ritz quotient, and the inequality itself follows from the Rayleigh-Ritz variational principle. In (RR), K and U are now functionals of trial eigenfunctions, and equality is obtained when the minimum of the Rayleigh-Ritz quotient is achieved, which occurs in variational calculations as the difference between the trial eigenfunction and the true eigenfunction approaches zero.
When looking for constraints on the density distribution , I first notice that for this problem the Rayleigh-Ritz quotient does not place any constraint on the scale of the density. Multiplying any particular mass distribution by a positive constant produces no change in this ratio, since the constant may be moved outside the integrals in both the numerator and the denominator and then cancels. This is an important difference between the present problem and the ones discussed previously (string vibration and traveltime inversion). The boundary of the feasible set is not found by scaling the density in this problem, and therefore the shape of the feasibility boundary is that of a cone in the model space.
However, an independent constraint on the density scale is easily obtained when the total mass M of a body such as the Earth is known, for then
_d= M. Another constraint on the overall scale is provided by the moment of inertia
To attack the inverse problem, I again introduce the concept of particular feasible density distributions and collections of these called ``feasible sets,'' as before. I assume that some subset of the modal frequencies has been measured. For simplicity, I display equations for only one frequency and trial eigenfunction, but understand that the same argument applies simultaneously to all eigenfrequencies and trial eigenfunctions. Suppose that and are two density distributions, both satisfying the Rayleigh-Ritz inequality for the same trial eigenfunction. Thus, I am considering only local or trial feasibility of the densities in this first example. Then, by assumption,
_n^2 _b K d_b U d both hold. If I next multiply (rho1) by and (rho2) by and add the two inequalities, I find
_n^2 _K d_U d, where is defined as the convex combination of the two densities. Thus, by the preceding argument, I have established the feasibility of the convex combination of any two density distributions that are themselves feasible (i.e., also satisfies the Rayleigh-Ritz constraints obtained from the data) for any particular choice of trial eigenfunction. This argument establishes that local feasibility sets are convex.
The proof is similar for global feasibility. Suppose I have found the actual eigenfunctions for the densities and , and therefore know the corresponding potential and kinetic energy densities Ka,Ua,Kb,Ub for these density distributions. These eigenfunctions (by assumption) produce minima in the respective Rayleigh-Ritz quotients; so if the resulting inequalities show that both and are feasible, then
_n^2 _a U_a d_a K_a d _a U_* d_a K_* d, and similarly
_n^2 _b U_b d_b K_b d _b U_* d_b K_* d, where the functionals K* and U* have been evaluated using some other convenient trial eigenfunctions (a specific choice will be made later in the discussion). Then, using the same argument as in the last paragraph, I find that the convex combination of densities must satisfy
_n^2 _U_* d_K_* d for any suitably constrained choice of trial eigenfunction. So, in particular the inequality must hold for the actual eigenfunctions that minimize the Rayleigh-Ritz quotient for (rhoGl*), i.e., when and .Thus, it follows from (rhoGl*) that if and are globally feasible densities, then so is their convex combination since
_n^2 _U_d_K_d. This proves that the global feasible set is convex. It is not hard to show that the global feasibility set may also be characterized as the intersection of all local feasibility sets, and is therefore a smaller (but still expected to be nonempty) set than any of the local feasibility sets (for particular trial eigenfunctions). It is harder to prove that the set is nonempty for this problem, than for the previous expamples.
CONSTRAINTS FOR ELASTIC MODULI AND DENSITY
Now suppose that the only data available for determining Earth structure is the free oscillation data. What can be said about the corresponding nonlinear inversion problem? It turns out that the analysis goes through essentially as before, but now the model space is larger, involving not only the density distribution but also the bulk modulus and the shear modulus .
The Rayleigh-Ritz inequality is still of the form
^2 (B + S) dK d. When two models and satisfy the feasibility constraints, I have
_n^2 _a K d(_a B + _a S) d and
_n^2 _b K d(_b B + _b S) d. And the convex combination
(_,_,_) (_a+(1-)_b, _a+(1-)_b,_a+(1-)_b) clearly satisfies the corresponding condition
_n^2 _K d(_B + _S) d, where the same trial eigenfunctions have been used in (model1)-(modelGl). This again establishes convexity of any local feasibility set and the proof of the convexity of the global feasibility set for follows immediately using the same arguments as before.
The Rayleigh-Ritz ratio is again scale invariant, so an overall change in scale of the form does not affect the frequency predictions. But, as long as the scale of any one of the parameters is known, the others follow from it, so knowledge of the total mass (totalmass) and/or total moment of inertia (totalmoment) is again sufficient to determine the scale of the model.
The main difference between the results for a single parameter and those for a set of parameters such as the triple is that, depending on details of how the three parameters are discretized for numerical treatment, the model space will be on the order of three times larger for the case of pure free oscillation data and therefore correspondingly more of this vibration data will be required to obtain enough constraints to produce the same degree of model resolution.
VARIATIONAL STRUCTURE OF INVERSE PROBLEMS
The various inverse problems considered so far may be viewed as special cases of the following general problem.
Suppose I have the set of measured data and that these data are known -- from the mathematical physics of the related forward problem -- to be minima of an appropriate variational functional so that
q_i Q_i[n_1,...,n_k, d_1,...,d_m; v_1,...,v_p], where Qi is a functional whose first (k+m) arguments are parameters of the model (such as density for string vibrations, slowness in traveltime tomography, or bulk and shear moduli in elastic vibration) and whose p remaining arguments are trial eigenfunctions. The dependencies on the trial eigenfuctions will be suppressed in the following discussion. If the functional can be written in the form of a quotient
Q_i[n_1,...,n_k, d_1,...,d_m] = N_i[n_1,...,n_k]D_i[d_1,...,d_m], where the functionals in the numerator Ni and in the denominator Di are themselves linear functionals of each of their arguments, then I find that all the examples considered may be written in this form (see Table 1).
It follows easily from this postulated form that the inverse problem leads in all cases to a convex feasible region in the multiparameter model space. This follows directly from the observation that, if
q_iD_i[d_1,...,d_m] N_i[n_1,...,n_k] for all i and if
q_iD_i[d_1,...,d_m] N_i[ñ_1,...,ñ_k] for all i, then for any in the range I find
q_i N_i[n_1^(),...,n_k^()]D_i[d_(), ...,d_m^()] for all i, where
n_j^() = n_j + (1-)ñ_j for 1 j k, and
d_l^() = d_l + (1-)d_l for 1 l m, guaranteeing that, if the ``hat'' and ``tilde'' models are themselves feasible for the given set of trial eigenfunctions, then the convex combinations of the ``hat'' and ``tilde'' models parametrized by are also feasible.
The argument just given depends strongly on the implicit assumption that the conditions for admissibility of eigenfunctions are independent of the convex combination parametrized by . Such independence is definitely true for the traveltime inversion problem where the ray paths play the role of eigenfunctions, but also definitely not true for the string density inversion problem or for the free oscillations problem. Thus, whether or not the global feasible set is convex depends on the problem, and in particular on the variational principle being used in the analysis. Rayleigh-Ritz variational problems will not have convex feasibility sets, while traveltime tomography and some other similar inversion problems [Berryman, 1991] in general do have convex feasibility sets.
1.25
Although convexity of the feasible set is not really necessary when designing a nonlinear programming method for solving the inverse problem, convexity does help to simplify the reconstruction algorithms when it is a characteristic of the problem of interest.
DISCUSSION
Finite data sets
Suppose I have a finite set of measurements and I compute the feasible set associated with that measurement set. Now suppose that an additional measurement is made so the measurement set is now with the associated feasible set . What is the relationship between and ? The addition of a constraint can only decrease the size of the feasible set, so it follows easily from the convexity properties that in general .
Measurement error
An issue that is often raised about the usefulness of the feasibility constraints concerns the effects of measurement errors on the location of the feasibility boundary. The variational constraint equations always find the data in the role of upper or lower bounds on integrals involving the unknown parameters. The data therefore enters these constraints linearly, so small measurement errors will generally lead to small (or possibly no) changes in the location of the bounding curves, depending on which measurements are in error and which measurements are the most constraining. I think of the feasibility boundary in these circumstances, not as a sharp but rather, as a fuzzy boundary. If the errors are small, then the fuzzy region is also small. It is useful to take this fuzziness into account in practical algorithms that make use of the feasibility boundary to reconstruct the desired model parameters in these inverse problems. This can be accomplished by using either the least (or the most) constraining range of data-minus-error (or data-plus-error) when computing this estimate of the boundary location. Alternatively, the fuzziness of the boundary can be incorporated directly into algorithms that use only the approximate location of the feasibility boundary as a means of constraining a search for the desired model parameters based on other criteria (such as minimizing the least-squares error in predicted versus measured data, or some other choices of objective functional minimization). Experience has shown that practical algorithms based on feasibility constraints are less sensitive (more robust) to the presence of measurement errors than most other algorithms for inversion.
Algorithms
The variational structure of nonlinear inverse problems does not by itself provide an algorithm for reconstructing the desired model parameters from the data. Nevertheless, knowing the existence of the feasibility boundary and the convexity properties of the feasible set suggests a number of possible algorithms that may be useful depending on the particular problem. I may suggest three types of algorithms: (1) The most obvious and probably the least practical algorithm entails a search along the feasibility boundary for the model that best fits the data. This approach has much in common with linear programming methods of the simplex type, but is probably not practical for most of the large dimensional problems that would benefit from the methods discussed in this paper. The reason for the difference is that the feasibility boundary in nonlinear inversion problems is determined only implicitly and therefore requires considerable computation to find each boundary point, whereas in linear and most other nonlinear programming problems the boundary constraints are given explicitly. (2) A Monte Carlo or shooting method that tries to sample a region of the model space and map the feasibility boundary in that local region has been tried on both the string density inversion problem and on the traveltime inversion problem. This approach has been found to work extremely well in the problems of lower dimensionality, and it also works well in higher dimensional problems that are easily parallelized (such as traveltime tomography) when many processors are available. Finally, (3) virtually any existing inversion algorithm can be easily modified to incorporate the feasibility constraints as a natural means of regularizing, i.e., preventing divergences from occurring. In particular, iterative linear least-squares inversion algorithms that might diverge due to inconsistencies arising from the forward modeling (trial eigenfuctions or trial ray paths) based on a previous guess of the model can be easily stabilized by forcing the stepsize for model updates to remain small enough so that the successive iterates do not wander away from the feasibility boundary. Such a constraint does not tie the result to any particular part of the model space that must be chosen prior to the inversion (i.e., hard constraints on the maximum and minimum values of the parameters in the model are not needed), but rather tethers the final result to a manifold determined strictly by the data and the measurement configuration. Thus, the data itself is used to determine the appropriate means of regularizing the solution to the inverse problem in such algorithms. This approach is probably the one that will find the most use in practical solutions to inverse problems.
ACKNOWLEDGMENTS
Numerical experiments for the string vibration problem were performed by O. S. Tai, a summer research student visiting at LLNL. I thank J. R. McLaughlin for insight into the general solution of the string vibration problem. I also thank G. C. Beroza, J. M. Rice, and G. Zandt for helpful leads into the literature on free oscillations of the Earth.
REFERENCES
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)