 |
Figure 1 DMO geometry for midpoint-offset coordinates.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTKinematically, Berryhill's ``pure migration'' or nonimaging shot-record migration is equivalent to dip moveout (DMO) before normal moveout (NMO) followed by Gardner's Prestack Imaging (PSI). The two processes have the same effect on a point diffractor in midpoint, offset, and time coordinates, compressing the Cheops pyramid surface to the same curve. The two methods produce the same kinematic result, although from a computational point of view, Berryhill's method is much faster. |
INTRODUCTION Prestack imaging (PSI) introduced by Gardner et al. (1986) is a prestack migration alternative. DMO followed by PSI migrates data without stacking. Gardner's claim to velocity independence is questionable, but it seems that by delaying the NMO step to the end of the processing flow, the data is better focused and it has a better signal to noise ratio.
Recently, Berryhill (1994), presented a new focusing technique called nonimaging shot-record migration based on the the idea that for a given shot and receiver position, data can be spread along a line instead of the conventional prestack migration ellipse. The method and the examples were presented for constant velocity, although Berryhill does mention the possibility of extending the principle to variable velocity.
The two methods are kinematically equivalent. I analyze the effect each method has on the reflection times from a point diffractor and show that both methods produce the same result. I start by reviewing Gardner's PSI and explain how the method reduces the Cheops-pyramid diffraction surface to a single curve. The resulting curve exists only in offset at the common-midpoint location above the diffractor. In other words the Cheops pyramid is compressed to a single curve in the common-midpoint section corresponding to the surface coordinate of the diffractor. Next, I analyze Berryhill's method and show that for the same diffractor, Berryhill's migration focuses the Cheops diffraction surface to the same curve generated by Gardner's method. Therefore, I conclude that the two methods are equivalent from a kinematic point of view.
Gardner's prestack imaging Gardner's Prestack Imaging (PSI) is a time migration process in common-midpoint, offset and time coordinates, based on focusing the Cheops-pyramid diffraction surface into a curve. To bring the Cheops surface to a suitable form for focusing, DMO before NMO is applied to the data. After DMO and PSI, the final image is obtained by NMO and stack.
 |
The equation for the source-receiver traveltime th
in the case of a single diffractor, schematically
represented in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , can be written as:
, can be written as:
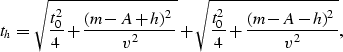 |
(1) |
A cut through the Cheops surface for a constant-offset,
produces the flat-top hyperbola curve shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For the zero-offset case,
the cut generates the customary zero-offset hyperbola
pictured on the face of the cube. As the offset increases,
the common-offset sections produced by setting the variable
h to a constant in equation (1), become
flat-top diffraction curves with apexes at increasing traveltimes.
. For the zero-offset case,
the cut generates the customary zero-offset hyperbola
pictured on the face of the cube. As the offset increases,
the common-offset sections produced by setting the variable
h to a constant in equation (1), become
flat-top diffraction curves with apexes at increasing traveltimes.
 |
The standard processing sequence of NMO followed by DMO
(or migration to zero-offset (MZO) in a single step)
transforms the flat-top hyperbolas into identical
zero-offset hyperbolas. Applying DMO before NMO
will produce zero-offset hyperbolas shifted down in time
with the NMO correction, as shown in the right cube
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . After the NMO correction,
the shifted zero-offset hyperbolas line up in offset,
and therefore stacking greatly improves the signal to noise ratio.
. After the NMO correction,
the shifted zero-offset hyperbolas line up in offset,
and therefore stacking greatly improves the signal to noise ratio.
After DMO-before-NMO, the diffraction curve th is given by
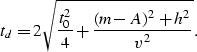
| |
(2) |
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Notice that in this formulation DMO is performed before
NMO (or alternatively inverse NMO is performed after MZO).
The hyperboloid
of revolution still includes the NMO correction.
This is made obvious
by rewriting equation (2) as
.
Notice that in this formulation DMO is performed before
NMO (or alternatively inverse NMO is performed after MZO).
The hyperboloid
of revolution still includes the NMO correction.
This is made obvious
by rewriting equation (2) as
![]()
 |
The essence of PSI is to sum over circles in time-slices.
The output of such a summation is represented on
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where the circle on the left side
is transformed into a single focused point on the right
side of the figure. The focused point is situated at the
apex of the semicircle. The summation algorithm can be any
choice of Kirchhoff or modified Stolt migration.
The end result of applying DMO before NMO, and PSI to
the Cheops surface, is a curve in the common-midpoint
section passing through A, the coordinate of the diffractor.
After NMO correction, the curve becomes a straight line
and can be summed over offset to obtain the image of the
point diffractor.
, where the circle on the left side
is transformed into a single focused point on the right
side of the figure. The focused point is situated at the
apex of the semicircle. The summation algorithm can be any
choice of Kirchhoff or modified Stolt migration.
The end result of applying DMO before NMO, and PSI to
the Cheops surface, is a curve in the common-midpoint
section passing through A, the coordinate of the diffractor.
After NMO correction, the curve becomes a straight line
and can be summed over offset to obtain the image of the
point diffractor.
The substance of this argument can be summarized in the fact that the result of applying DMO before NMO and PSI to the Cheops surface, reduces this surface to a hyperbola located in the common-midpoint gather containing the model diffractor. After NMO correction, the hyperbola becomes a line, positioned in time at the zero-offset traveltime t0.
Berryhill's pure migration Berryhill (1994) presented a new migration algorithm he calls ``Nonimaging Shot-Record Migration'' based on spreading the energy along a line in a common-shot section. The line represents the two-way shot traveltime in a constant velocity medium. The proof that for a source-receiver geometry the source traveltime is a line, is given in Appendix A. The equation of the line is shown to be:
| |
(3) |
The essence of the method is that spreading data over the time
and surface coordinates in
equation (3) focuses the hyperbola generated
by a single diffractor in a common-shot record.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is an example of applying Berryhill's
migration to a common-shot record over a point diffractor.
Figure
is an example of applying Berryhill's
migration to a common-shot record over a point diffractor.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a displays
the input to Berryhill's migration and Figure
a displays
the input to Berryhill's migration and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
displays the result of spreading data over the lines
given by equation (3).
In Appendix B I prove that the surface coordinate of the focusing
point corresponds to the surface coordinate of the diffractor,
and the time to the focusing point is twice the shot-time.
b
displays the result of spreading data over the lines
given by equation (3).
In Appendix B I prove that the surface coordinate of the focusing
point corresponds to the surface coordinate of the diffractor,
and the time to the focusing point is twice the shot-time.
 |
The code used to produce Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b is very simple.
The first two loops parse the data in space and time. The third loop
parses the output in space and identifies for each input data
point the time and space coordinates of the output line.
The body of the Fortran kernel can be summarized as:
b is very simple.
The first two loops parse the data in space and time. The third loop
parses the output in space and identifies for each input data
point the time and space coordinates of the output line.
The body of the Fortran kernel can be summarized as:
 |
The data used for Berryhill's migration is taken from a single
shot record, but the surface coordinates are the common-midpoints.
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where I tried to reproduce the same
image as the one in the original Berryhill paper, the depth
of the diffractor is 1406 meters, and the surface coordinate
of the diffractor is -800 meters. The velocity used is 2800 meters
per second. However, because data is represented in common-midpoint
surface coordinates, in Figure
, where I tried to reproduce the same
image as the one in the original Berryhill paper, the depth
of the diffractor is 1406 meters, and the surface coordinate
of the diffractor is -800 meters. The velocity used is 2800 meters
per second. However, because data is represented in common-midpoint
surface coordinates, in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the top of
the diffraction hyperbola is situated at -400 meters and not
-800 meters, as it would be in a shot record. The focusing
point after migration is located at the common-midpoint location
of -800 meters, corresponding to a half offset of 800 meters.
As a result, after resorting the prestack data in common-midpoint
and offset coordinates, the shot record that constituted the input,
contributes a single trace to the output dataset, with midpoint
-800 and half offset -800. For a shot located at -800, after
Berryhill's migration, the focusing point is situated
at the same location but at half-offset zero.
,
the top of
the diffraction hyperbola is situated at -400 meters and not
-800 meters, as it would be in a shot record. The focusing
point after migration is located at the common-midpoint location
of -800 meters, corresponding to a half offset of 800 meters.
As a result, after resorting the prestack data in common-midpoint
and offset coordinates, the shot record that constituted the input,
contributes a single trace to the output dataset, with midpoint
-800 and half offset -800. For a shot located at -800, after
Berryhill's migration, the focusing point is situated
at the same location but at half-offset zero.
For more shot-record migrations, the surface coordinate of the focusing
point remains unchanged but the time coordinate increases with offset.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represents a sketch of the
focusing geometry over a single point diffractor, after
Berryhill's migration, for two different shot
locations.
Both migrations focus the
diffraction hyperbola at the same surface location, but
at different times. After NMO correction, the time is
identical for all the shot records. Therefore, in common-midpoint
and offset coordinates, the output of Berryhill's migration is
a curve passing through the surface coordinate of the
diffractor. The curve is situated in the common-midpoint
gather containing the diffractor, exactly like the output
of PSI, and is shifted down in time with the NMO correction,
again, precisely like the output of PSI.
represents a sketch of the
focusing geometry over a single point diffractor, after
Berryhill's migration, for two different shot
locations.
Both migrations focus the
diffraction hyperbola at the same surface location, but
at different times. After NMO correction, the time is
identical for all the shot records. Therefore, in common-midpoint
and offset coordinates, the output of Berryhill's migration is
a curve passing through the surface coordinate of the
diffractor. The curve is situated in the common-midpoint
gather containing the diffractor, exactly like the output
of PSI, and is shifted down in time with the NMO correction,
again, precisely like the output of PSI.
CONCLUSIONS Since the two methods, Berryhill's ``pure migration'' and DMO followed by Gardner's PSI, produce the same image given the same input, I conclude that the two methods are kinematically equivalent. Berryhill's method opens to research interesting questions like the velocity sensitivity of the method, the phase-shift equivalence of the algorithm, the full extraction of the operator amplitudes from the wave equation, and the formulation of an adjoint operator for modeling.
I benefited from helpful discussions with Dimitri Bevc, Jon Claerbout, and John Berryhill. Andrei Popovici pointed out a flaw in my algebra, thus helping me to finish the mathematical demonstrations.
REFERENCES
APPENDIX A This appendix demonstrates that for a fixed shot-receiver geometry, the traveltime from the shot location to any point on the migration ellipse is a line. In other words an impulse which is spread over an ellipse in common-offset prestack migration can be spread over a straight line in shot-record migration.
 |
The time from the shot to the ellipse and back, ts, is defined as
| |
(4) |
![]()
![]()
![]()
![]()
| v4th4+(4h2-4hxs)2-2v2th2(4h2-4hxs)= 4v2th2(xs2+zs2). | (5) |
Introducing the right side of equation (5) in the equation for the double shot time (4) becomes:
![\begin{displaymath}
\begin{array}
{lcl}
{{v^2 t_s^2} \over 4} & = & x_s^2+z_s^2
...
..._h}\over 2}-{(4h^2-4hx_s) \over {2vt_h}} \right]^2}.\end{array}\end{displaymath}](img12.gif) |
(6) |
And finally for the shot time ts I obtain Berryhill's migration line:
| |
(7) |
APPENDIX B The purpose of this appendix is to demonstrate that using the Berryhill migration algorithm, a diffractor curve in a shot-record is focused to a point with the same surface coordinates as the diffractor. The time coordinate of the focusing point corresponds to twice the traveltime from the source to the diffractor. Suppose the diffractor is located at a distance xd from the shot, at a depth zd. For simplicity the shot is considered to be at the origin of coordinates. The traveltime th from the shot to a receiver situated at a distance 2h from the shot is:
![]()
![]()
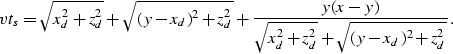 |
(8) |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example of the family of lines
described by equation (8). Each line corresponds to
a fixed value of y and passes through the corresponding value
of th. The lines have the remarkable property of passing through the
same point xs. We can easily find the value of xs by solving
equation (8) for two different values of y, for
example y1=0, y2=2xd. For x=2xd equation (8)
becomes independent of y:
shows an example of the family of lines
described by equation (8). Each line corresponds to
a fixed value of y and passes through the corresponding value
of th. The lines have the remarkable property of passing through the
same point xs. We can easily find the value of xs by solving
equation (8) for two different values of y, for
example y1=0, y2=2xd. For x=2xd equation (8)
becomes independent of y:
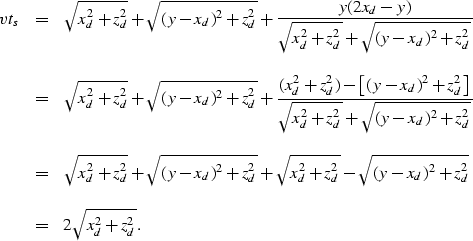 |
(9) |
The shot-time for x=2xd is constant for any value of the
offset y=2h. Since the surface coordinates in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are the common midpoint positions,
the diffractor is focused at the correct surface position xd,
for a half-offset equal to the surface distance from the shot to
the top of the diffractor x=xd.
For this geometry, the NMO correction from ts to zero-offset
time t0 gives us
are the common midpoint positions,
the diffractor is focused at the correct surface position xd,
for a half-offset equal to the surface distance from the shot to
the top of the diffractor x=xd.
For this geometry, the NMO correction from ts to zero-offset
time t0 gives us
![]()
 |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)