Preconditioning the wave equation

Martin Karrenbach

martin@sep.stanford.edu

ABSTRACT

The solution of systems of equations can employ preconditioning of the involved operators. This preconditioning process aims at accelerating convergence and requires some estimate of the solution or of the operator behavior. I outline a preconditioning operation for use with wave equations having the aim of increasing the region of stability of the evolution equation.

A well known mathematical/numerical tool in solving large systems of equations is the use of a preconditioner. Nichols outlines the characteristics of the left and right preconditioner for an algebraic system of equations. I try to extend this method from its inversion problem setting to the wave equation setting and reinterpret its consequences. Following expositions by Tal-Ezer , I am trying to find an efficient preconditioner for solving wave equation problems. A proper preconditioner for wave equation problems should ideally help with two aspects, namely stability and accuracy. Numerical dispersion is viewed as part of the accuracy problem.

THE GENERAL WAVE EQUATION A general second order wave equation can be written as

$$u_{tt} = D u + s , \EQNLABEL{full}$$ (1)

where $D={1\over{\rho}}\nabla C \nabla^{t}$ represents the spatial derivative operator, which incorporates medium properties such as elastic stiffness and density. The last term is the source term s. Given a set of boundary conditions, equation full specifies a differential problem completely. However, when we want to solve that problem numerically for a large number of grid points, it becomes crucial to determine an efficient way in which to solve that equation. Discretization in time and space will determine the accuracy and stability of that method.

In the following, let us look at the time evolution problem, but keep in mind that it actually represents any general evolution/extrapolation problem. One will then seek to solve a related problem using an operator P

$$u_{tt} = P ( D u +s ) \EQNLABEL{pregen}$$ (2)

that will have approximately solution u, but will allow a coarser and thus more accurate time integration scheme.

THE GENERAL FORM The task for P, where $P(\epsilon)$ is a parametric preconditioner, is as always, to decolor the right hand side of equation full. P is a system of preconditioners and we can see what the preconditioner does to the original solution u by expanding equation full

$$\partial_t^2 u = \tilde P ( D u + s ) + (I - \tilde P) ( D u + s ) \EQNLABEL{expanded}$$ (3)

If the last term is dropped with the argument that $I - \tilde P$is assumed to be very small, we get the preconditioned problem pregen. In this general notation

$$P = {1\over{(s + \epsilon D u )}}$$ (4)

or, following the same reasoning as before, according to which we wanted to decolor the right-hand side independent u and s, we get

$$P = (1+\epsilon D)^{-1}.$$ (5)

In the most general case the preconditioner P will depend on the discretization of the derivative operator, the medium, and thus on the wave types within the medium. However, a simple representation can still be found that should allow increased range of stability and accuracy.

In order to understand the problem, one can simplify it to include only one wave type (scalar problem) in one space dimension. Equation full reduces then to the familiar:

$$u_{tt} = v^2 {\partial^2_x} u + s \EQNLABEL{scalar1d}$$ (6)

Assuming one would like to extrapolate equation scalar1d in time, we are confronted with a basic problem resulting from the nature of this equation. First, the source term has a certain frequency content that gets injected at each time step. Second, the medium is characterized by a heterogeneous velocity v that introduces potentially high spatial wave numbers. Thus the solution to this equation is possibly highly oscillatory.

Imagine for a moment that for some reason the right hand side of equation scalar1d is not oscillatory, but smooth. If this thought is taken to the extreme, it could be a constant function. Then, extrapolating u would be easy, since we know how to extrapolate a constant function. In reality, we will hardly be able to get the right hand side of equation scalar1d to be constant, except for very special media and special sources. However, we could recast the problem scalar1d and solve a slightly different problem

$$u_{tt} = Q\, ( v^2 {\partial^2_x} u + s ) . \EQNLABEL{scalarpre1d}$$ (7)

We can now ask ourselves, how we could choose Q such that extrapolation of equation scalarpre1d is quick and efficient, despite the fact that v might be blocky, discontinuous, and heterogeneous and u highly oscillatory. If $Q\, ( v^2 {\partial^2_x} u + s )$ would be smooth, then u_tt and u would be band-limited and low frequency, and predictability along the extrapolation axis would be good. For example, a sinusoid is predictable and can be extrapolated without much of a problem.

Taking this idea to the extreme would require us to have Q such that $Q\, ( v^2 {{\partial^2}\over{\partial_x}} u + s )$is a constant function. How to extrapolate a constant function would now be self-evident.

We see then what the preconditioner for the wave equation extrapolation should do: effectively lower the frequency content in $\quad ( v^2 {\partial^2_x} u + s )$in such a way that the extrapolation is stable in larger regions and thus allows us to take bigger time steps with higher accuracy.

THE CHOICE OF PRECONDITIONER

Accepting the previously outlined role of the function Q as a preconditioner, we are faced with the problem of how to determine Q in reality. What Q should we actually use for preconditioning? Clearly the source term s and the spatial operator in equation scalar1d influence the choice. More specifically, it is the temporal and spatial frequency of the source term s and the spatial frequency content of the discretization of the medium operator $v^2 {\partial^2_x}u$.Obviously, choosing Q to satisfy

$$Q = {const \over{ v^2 {\partial^2_x} u + s }} \EQNLABEL{fullprecon}$$ (8)

would decolor the entire right hand side. The problem however is that Q requires the knowledge of the solution u and the source term s. In reality the source s is known, but the solution is not. Equation fullprecon would mean we had already found the solution to the entire problem, which is clearly not true in a modeling problem. For preconditioning we only need an estimate that gets us closer to the solution.

Choosing Q = s^-1 would decolor the source completely, but would not modify contributions that are introduced by the medium operator D. Clearly, the source s and the solution u are not totally independent, but we can always argue that the frequency content of u is similar to s modulo contributions from the medium operator term. A preconditioner that would attempt to decolor the right hand side under the assumptions that the frequency content of u and s is similar to

$$Q = \left( { 1 \over {1 + v^2 \partial^2_{x} } } \right) {1 \over a} \EQNLABEL{splitprecon}$$ (9)

still contains the amplitude spectrum a of solution and source term. Again this preconditioner contains knowledge of u and s (at least the spectrum). For modeling time evolution, we would like to have a preconditioner that is free of an estimate of the solution.

Retaining only the first factor in equation splitprecon, we get a preconditioner that only depends on the medium operator itself, namely

$$Q = { 1 \over {1 + v^2 \partial^2_{x} } } \EQNLABEL{mediumprecon}$$ (10)

A PARAMETRIC PRECONDITIONER Equation mediumprecon gives preconditioner Q that is fixed for the entire evolution problem. Since the evolution problem is not like an optimization problem, we might argue that a variation of the preconditioner during the evolution process is a good idea. This is true, of course, if we have a strategy of choosing Q appropriately, such as to increase convergence, accuracy or stability. A reasonable choice is the form

$$Q = { 1 \over {1 + \epsilon v^2 \partial^2_{x} } } , \EQNLABEL{epsprecon}$$ (11)

where $\epsilon$ is a small parameter in the range of [0,1]. Choosing $\epsilon$ to be would mean that we solve the unconditioned problem and that $\epsilon$ equals 1 equals the fully conditioned one. The adjustment of $\epsilon$ can be chosen optimally.

SHAPE OF PRECONDITIONERS In the previous paragraph we saw how a preconditioning operator can be chosen for a wave propagation problem. But, now that we know how to design a preconditioning operator, we are faced with the problem of how to apply it. In this section I explain an approximation procedure and in the next I show how to apply it implicitly, but exactly.

Take again the parametric preconditioner epsprecon that can be discretized with a simple second order stencil in one space dimension:

$$( 1 + \epsilon v^2 \partial^2_{x} ) = 1 + \epsilon \pmatrix... ... \cr & & & v^2_{n-2} & -2 v^2_{n-1} \cr } \EQNLABEL{simplemat}$$ (12)

This operator is tridiagonal and also diagonally dominant, and for $\epsilon=0$ it is the identity operator. For the preconditioner, we are seeking the inverse of operator simplemat. Unfortunately, the inverse has not as satisfactory a structure as operator simplemat itself, but is less dense and thus less efficient to implement.

Accepting the fact that we want to approximate efficiently the inverse of operator simplemat, we can try it using another tridiagonal matrix

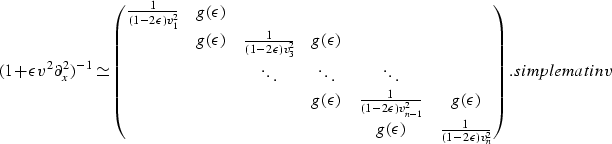$$( 1 + \epsilon v^2 \partial^2_{x} )^{-1} \simeq \pmatrix{ {... ...& {1}\over{(1-2\epsilon) v^2_n} \cr } . \EQNLABEL{simplematinv}$$ (13)

This form can again be applied quite efficiently. One could even think of dropping the off-diagonal terms, but that would correspond only to a diagonal scaling and the preconditioning effect would be reduced.

PRECONDITIONERS AND IMPLICIT SOLUTIONS An alternative to using an approximation such as equation simplematinv is to solve equation scalarpre1d implicitly. Consequently, we would solve it in the following form

$$(1 + \epsilon v^2 \partial^2_{x} ) u_{tt} = \quad ( v^2 {\partial^2_x} u + s ) . \EQNLABEL{scalarpreimplicit}$$ (14)

Pulling out the time derivative sheds some light on how the original equation scalar1d is modified by preconditioning.

$$\partial^2_t { u + \epsilon v^2 \partial^2_{x} \partial_t^2 u = \quad ( v^2 \partial^2_x} u + s ) . \EQNLABEL{preimp}$$ (15)

With a simple second order time stepping we can see what is typically involved in solving this equation for the n+1st time step.

$${(1 + \epsilon v^2 \partial_x^2) u^{n+1}} = (1 + \epsilon v^... ...\Delta t}^2 ( v^2 \partial_x^2 u^n + s^n ). \EQNLABEL{timestep}$$ (16)

As can be seen in equation timestep, we have to solve implicitly for a uⁿ⁺¹. It is a system of simultaneous equations where u_iⁿ⁺¹ are coupled spatially depending on the spatial discretization operator $v^2 \partial^2_x$, such that the number of unknowns corresponds to the number of convolution coefficients in the operator. We solve that system at each time step. Thus implicit time stepping can be viewed as an implicit preconditioning of the solution to the original wave equation.

Solving the wave equation implicitly is only efficient if the time step can now be chosen to be larger than the explicit solution would give. However, the solution of the system of equations at each time step slows the algorithm down. Consequently, there is a potential inefficiency. Note also the similarity of the implicit preconditioner to methods such as Crank-Nicholson.

MORE THAN ONE DIMENSION In the previous sections I restricted myself to a wave propagation problem in one space dimension in order to give illustrative examples. In 2D or 3D the scalar wave equation illuminates still some more interesting points. The 3D scalar wave equation takes on this form

$$\partial_t^2 u = ( \partial_x^2 + \partial_y^2 + \partial_z^2 ) u + s .$$ (17)

Thus a preconditioner analogous to equation mediumprecon is now

$$f = {1\over{ 1 + \epsilon v^2 ( \partial_x^2 + \partial_y^2 + \partial_z^2 )}} \EQNLABEL{nonsplit}$$ (18)

This preconditioner operates on all spatial dimensions simultaneously and as an approximation, we can think of representing it as a split operator of the form

$$f = ({1\over{ 1 + \epsilon v^2 \partial_x^2}}) ({1\over{ 1 ... ... ({1\over{ 1 + \epsilon v^2 \partial_z^2}}) \EQNLABEL{splitpre}$$ (19)

This corresponds to a cascade of operators of the form epsprecon.

Choosing $\epsilon$ optimally During the time stepping the preconditioner can be varied, in particular via the small parameter $\epsilon$. As an upper bound one can require that $\epsilon$ has to be chosen such that the energy in the timestepped terms is less than some tolerance $\delta$

$${{\vert\vert (I-P)( D u^n + s^n) \vert\vert}\over{ \vert\vert P( D u^n + s^n)\vert\vert}} \le \delta$$ (20)

A similar solution is

$$\begin{eqnarray} \tilde D = P D \\ \tilde s = P s \\ \partial_t^2 u = \tilde D u + \tilde s .\end{eqnarray}$$ (21) (22) (23)

corresponding to Dave's right-preconditioner. Here the operator D together with the source s is preconditioned and the original wave equation is used unmodified.

Wave propagation problems can be tackled using the numerical tool of preconditioning. The task of a preconditioner in a wave propagation setting is to increase for a numerical solution the range of stability and rate of convergence to the correct solution. In solving evolution equations an efficient preconditioner has to be found that depends on the discretization of the spatial medium operator. Implicit solutions of wave equations implicitly precondition the original problem. Second order scalar wave equations in 1D serve as illustrative examples and lead to a general preconditioning formulation for general wave propagation problems.

I enjoyed working together with SEP's visitor Hillel Tal-Ezer from Tel Aviv University, who pointed me in the direction of preconditioning partial differential equations.

[SEP,paper]