![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTA new approach to computing traveltimes and ray paths by solving the shortest path problem is presented. The technique is based on a partitioning of the shortest path optimization problem into smaller problems. We recursively evaluate the solution on expanding wavefronts instead of finding the global shortest paths from the source. To solve the local minimization, we apply a modified version of the Bellman-Ford optimization algorithm because of its suitability for a parallel implementation in three dimensions. |
Traveltime calculations and ray path information play an important role in many methods of seismic data processing such as migration, tomography and modeling. For any three-dimensional application of these processing tools, an efficient use of computer resources becomes paramount. A process such as prestack migration, for example, requires calculating Green functions, which depend on the traveltimes between survey points on the surface and depth points in the velocity model for every surface (source or receiver) location. Moreover, in nonlinear seismic tomography and velocity inversion, ray tracing is the most time-consuming step.
Traveltimes and ray paths are often computed by ray tracing (), ray bending (), or shooting rays (). These methods can produce the correct answer but are computationally intensive, frequently encounter shadow zones, and sometimes pick the wrong ray path as the first arrival.
Several new methods for calculating first-arrival traveltimes and ray paths have recently been published. Vidale , Podvin and Lecomte , and van Trier and Symes used different versions of finite-difference approximations to the eikonal equation to estimate first arrival traveltimes on a regular grid.
Moser and Fischer and Lees calculate seismic ray paths by using graph theory to find the shortest path traveltimes on a network that represents the model of the earth. The advantages of this approach is that it always finds the global minima. Problems associated with convergence to local minima, as in ray bending, are thus avoided.
Inspired by this new method of shortest path ray tracing, we present an efficient, shortest path traveltime computation method that will determine accurate first arrival traveltimes through arbitrary, discrete, and discontinuous velocity models. The method is a modified version of the Bellman-Ford algorithm (see Bertsekas and Tsitsiklis, 1989) used for solving shortest path problems. We chose to use this algorithm because of its suitability for a parallel implementation in three dimensions.
Our traveltime computation procedure advances radially across a polar grid, computing first arrival traveltimes and ray paths, shell by shell, as it goes. At any stage during the mapping, only the outer traveltimes of a shell are used to calculate new traveltimes of the next shell. The traveltime computation scheme and our modification to the Bellman-Ford algorithm, which decrease the computational requirements, are presented in detail in this paper from a theoretical standpoint. Implementations of this method will be discussed in a future SEP report.
THE SHORTEST PATH PROBLEM AND SEISMIC RAY PATHS
The shortest path problem is a classic and important combinatorial problem that
arises in many contexts. There are many applications of the shortest path problem.
As Moser points out, ``They are usually of a discrete nature:
there are a finite number of objects, and the exact solution of the problem can be
found in a finite number of steps.'' The shortest path problem is defined in terms
of a directed graph consisting of n nodes, which are numbered ![]() . Node
is called the ``source''. We are given a scalar aij for each arc (i,j), which we
call the weight or ``length'' of (i,j). The length of a path
. Node
is called the ``source''. We are given a scalar aij for each arc (i,j), which we
call the weight or ``length'' of (i,j). The length of a path
![]() from node i to node j
with arcs
from node i to node j
with arcs ![]() is defined to be the sum
of the arc lengths
is defined to be the sum
of the arc lengths ![]() . The problem
is to find a path of minimum length (or shortest path) from the source to every node i.
. The problem
is to find a path of minimum length (or shortest path) from the source to every node i.
Seismic ray paths are approximated, based on Fermat's principle, by shortest paths for the problem of computing first arrival traveltimes. The model of the earth is represented by a network, consisting of nodes connected by arcs. Each arc is assigned a length equal to the ray's traveltime along the arc. The networks used to represent velocity models in this paper are sparse; i.e., each node is connected with a restricted number of nodes in its neighborhood but not with points that lie farther away. This neighborhood is called the node's adjacency-list and contains all the nodes such that there exists an arc that connects them.
The shortest path problem can be solved for any parameterization of
the velocity model and any arrangement of the nodes as long as there
exists a path from every node ![]() to the source node. In
our implementation of the shortest path problem we have chosen to use
a polar parameterization, assigning a constant velocity inside each
polar cell. Just as Fischer and Lees ,
we distributed the nodes regularly at the boundaries of the cells
(Figure network). Two nodes are connected only when there is no
cell boundary between them. The traveltime between two connected nodes
is defined as their Euclidean distance multiplied with the slowness of
the cell in between. As suggested by Fischer and Lees, the choice of
models with constant velocity cells has the welcome advantage of
particularly simple and fast calculation of traveltimes between
connected nodes; a lookup table can be used.
to the source node. In
our implementation of the shortest path problem we have chosen to use
a polar parameterization, assigning a constant velocity inside each
polar cell. Just as Fischer and Lees ,
we distributed the nodes regularly at the boundaries of the cells
(Figure network). Two nodes are connected only when there is no
cell boundary between them. The traveltime between two connected nodes
is defined as their Euclidean distance multiplied with the slowness of
the cell in between. As suggested by Fischer and Lees, the choice of
models with constant velocity cells has the welcome advantage of
particularly simple and fast calculation of traveltimes between
connected nodes; a lookup table can be used.
networkwidth=3.in.Network of nodes and arcs. Solid dots represent nodes in the graph, which are placed on cell boundaries (dotted lines). Arcs are represented by solid lines. The upper-left cell shows all the arcs that lie within that cell. On the right side we show the adjacency-list of the node in the middle. Adapted from Fischer et. al. (1993).
THE BELLMAN-FORD ALGORITHM
Moser, and Fischer and Lees solved the single source shortest path problem using the modified Dijkstra algorithm (see Cormen et. al., 1990). Dijkstra's algorithm maintains a priority queue that contains nodes for which the shortest path from the source has not yet been computed. In the modified Dijkstra algorithm this priority queue is implemented as a binary heap. In both methods, the algorithm inflicts a heavy toll on computer resources, both in memory and time, which may prevent it from being used seriously in 3-D applications. The method we have chosen to solve the single source shortest path is the Bellman-Ford algorithm, with which we address these difficulties.
Bertsekas and Tsitsiklis show that
the shortest path lengths xi*, ![]() are the unique
solutions of the system
are the unique
solutions of the system
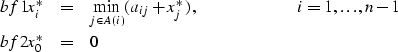 |
(1) | |
| (2) |
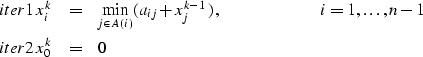 |
(3) | |
| (4) |
Note that the Bellman-Ford algorithm is particularly well suited for parallel and distributed implementations since the iteration for each node i can be carried out simultaneously with the iteration for every other node.
Regarding initial conditions, one possible set of initial conditions in the Bellman-Ford
algorithm is ![]() for
for ![]() and x00 = 0. Another possible
set of initial conditions can be obtained for certain applications where the
shortest path problem must be solved repeatedly, since the arc lengths change by small
increments. A small change in the arc lengths implies a small change in the shortest
path lengths, so it may be advantageous in terms of convergence speed to restart the
Bellman-Ford algorithm, using as initial conditions the previous shortest path lengths.
This would be the case in which we have a certain number of sources spaced closely
enough so that the paths the seismic rays follow change by small increments for two
contiguous source locations.
and x00 = 0. Another possible
set of initial conditions can be obtained for certain applications where the
shortest path problem must be solved repeatedly, since the arc lengths change by small
increments. A small change in the arc lengths implies a small change in the shortest
path lengths, so it may be advantageous in terms of convergence speed to restart the
Bellman-Ford algorithm, using as initial conditions the previous shortest path lengths.
This would be the case in which we have a certain number of sources spaced closely
enough so that the paths the seismic rays follow change by small increments for two
contiguous source locations.
Modified Bellman-Ford Algorithm
We derive a more efficient Bellman-Ford algorithm by iterating equation iter1 only on the nodes that belong to a certain shell. Once the algorithm converges on this shell it goes on to the next outer shell. Figure iter depicts the steps followed by the modified Bellman-Ford algorithm. Equations miter1 and miter2 define the new algorithm
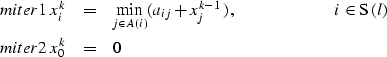 |
(5) | |
| (6) |
iterheight=3.15in.Four steps (a,b,c,d) with the modified Bellman-Ford implementation for a very simple model. The model is represented by two polar cells per shell. Step (a) shows the initial conditions. Solid dots represent nodes for which we have calculated shortest path traveltimes. White dots represent nodes for which we have not computed its shortest path traveltimes. In steps (b,c, & d) the algorithm iterates for each shell to find the shortest path traveltimes of the nodes that belong to that shell (polka-dotted dots).
The traveltimes to the first ring of nodes (Figure itera) are computed by tracing straight rays from the source to these nodes. At each step, the algorithm computes the shortest path traveltimes to the nodes of one particular shell. At the next step, the algorithm finds the traveltimes to the nodes belonging to the next contiguous outer shell. In this implementation, nodes are only connected if they obey the following two rules:
Thus, at each iteration, a node sitting on the outer boundary of a shell cannot connect with nodes that lie radially further away. This condition reduces the size of the adjacency-list of these nodes, which translates into fewer iterations for finding the minimum function in equation miter1. A drawback is that we are eliminating overturned rays. However, we reduce this problem by using a polar coordinate frame.
The use of polar coordinates has the disadvantage of the extra cost of mapping velocity and traveltime fields to and from polar coordinates. Nevertheless, polar coordinates have been successfully used in finite difference traveltime calculation (). These coordinates have the advantage of providing a frame that matches the constant velocity wavefronts. Even in variable velocity models, the computational grid for polar coordinates better matches wavefronts than a rectangular grid does.
In implementing the Bellman-Ford algorithm in a ``shell by shell'' way, we reduce the amount of memory resources that the algorithm needs, since the modified version needs to keep in memory at one time only the information concerning the nodes of a shell, while in the original version or in Dijkstra's algorithm, we need to allocate memory for all the nodes of the model.
For a parallel implementation of the modified Bellman-Ford algorithm, only the iterations of nodes that belong to a particular shell are computed simultaneously. A comparison of the Bellman-Ford algorithm with the modified version shows that the latter has the advantage of needing only to broadcast a smaller copy of the vector xk-1 to each running processor. While in the original algorithm this vector has the size of the total number of nodes, in the modified algorithm it only requires the nodes per shell.
Traveltimes at receivers
In order to generate the traveltime tables, the algorithm takes only the values of the shortest path traveltime computed for those nodes that lie on curved boundaries (see Figure inter). Since these nodes are regularly distributed on a polar grid, as shown in the Figure, the algorithm outputs these values directly. Finally, the output of the algorithm is piped into a separate program that does a bilinear interpolation of the traveltime tables in order to map them from polar coordinates to rectangular coordinates.
Note that radially aligned nodes are only used in the algorithm to allow rays to bend, while they are not used in the generation of the traveltime tables.
interheight=3.3in.Final traveltime table (b) on a polar frame. (a) shows a set of nodes for which we have already computed the shortest path traveltimes. Out of these nodes we pick those that lie on the curved boundaries (polka-dotted dots) to build the final traveltime table. Radially aligned nodes (solid dots) are necessary for rays to bend.
The modified Bellman-Ford algorithm allows an efficient computation of ray paths and traveltimes by computing them over expanding wavefronts. By partitioning the global problem of finding the shortest paths from a source, into smaller problems, we obtained an algorithm that is more computationaly efficient. The method constructs a global traveltime and ray field to all points in space, so there are no problems with shadow zones. A parallel implementation of the algorithm should prove very useful for three dimensional applications.
[hector,SEP,GEOTLE]
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)