

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
ifundefinedJimInclude
falsetrue
falsetrue
Stress-induced transverse isotropy in rocks
Lawrence M. Schwartz,![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) William F. Murphy, III,
William F. Murphy, III,![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
and James G. Berryman
Author has no known email address
ABSTRACT
The application of uniaxial pressure can induce elastic anisotropy
in otherwise isotropic rocks. We consider models based on two very
different rock classes, granites and weakly consolidated granular
systems. We show (1) that these models share common underlying assumptions,
(2) that they lead to similar qualitative behavior, and (3) that both provide
a microscopic basis for elliptical anisotropy. In contrast,
a finely layered transversely isotropic medium always shows anelliptical
anisotropy. In the granular case,
we make experimentally verifiable predictions regarding the horizontally
propagating modes based on the measured behavior of the vertical modes.
|
INTRODUCTION
It is well known that the elastic properties of the rocks comprising the
earth's sub-surface are highly non-linear (Walsh, 1965a,b,c).
In terms of seismic and sonic wave propagation, the signature of this
non-linearity is the pressure dependence of the P and S sound speeds.
An additional complication is the fact
that the sub-surface pressure environment is often
anisotropic. Accordingly, it is essential for the proper
interpretation of both seismic and sonic measurements that we
have a semi-quantitative understanding of the effects of stress
anisotropy.
In the present paper we examine the uniaxial response of systems whose
elastic properties are isotropic under the application of hydrostatic
stress. While the P and S velocities of such systems exhibit clear
pressure dependence, the VP/VS ratio is often independent of the
applied pressure (Domenico, 1977). However, once the applied stress is
uniaxial, these
systems exhibit transversely isotropic (TI) behavior and the three
VP/VS ratios depend on the applied stress (Nur and Simmons, 1969;
Murphy, 1982; Zamora and Poirier, 1990; Yin and Nur, 1992).
We study two distinct types of models that predict pressure induced
velocity anisotropy in rocks: (1) granular materials under combined
hydrostatic plus uniaxial loading and (2) rocks with randomly oriented
cracks under uniaxial loading. The first class of models was
developed by Schwartz et al. (1984), Schwartz (1984),
and Walton (1987) and is appropriate for
weakly consolidated granular materials. The second model was
developed by Walsh (1965a,b,c) and Nur (1969; 1971) to describe the
properties of granites. While these models are directed toward very
different rock classes, we will see that the physical bases
of the induced anisotropy are quite similar, as are their qualitative
predictions.
In the model developed by Walsh (1965a,b,c) and Nur (1969; 1971), the rock
is represented by an isotropic array of penny-shaped cracks. Under uniaxial
compression, the normal stress acting on each contact is assumed to vary as
| 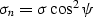 |
(1) |
where 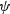 is the angle between the crack normal to the stress axis.
Basically, the
is the angle between the crack normal to the stress axis.
Basically, the 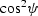 dependence is the simplest variation
that is consistent with the symmetry of the problem. As the value of
dependence is the simplest variation
that is consistent with the symmetry of the problem. As the value of
 is increased, cracks oriented with their normals close to the
pressure axis close and the elastic properties of the rock
become anisotropic. In
the granular models developed by Schwartz (1984), adjacent grains
are coupled (at their contacts) by effective normal and tangential
springs with force constants Dn and Dt. Once again, under
uniaxial stress, these quantities are assumed to vary as
is increased, cracks oriented with their normals close to the
pressure axis close and the elastic properties of the rock
become anisotropic. In
the granular models developed by Schwartz (1984), adjacent grains
are coupled (at their contacts) by effective normal and tangential
springs with force constants Dn and Dt. Once again, under
uniaxial stress, these quantities are assumed to vary as
| ![\begin{eqnarray}
D_n = D^{(0)}_n \left[ 1 + \delta \cos^2 \psi \right],\nonumber\\ D_t = D^{(0)}_t \left[ 1 + \delta \cos^2 \psi \right],
\end{eqnarray}](img5.gif) |
|
| (2) |
Here 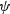 is now understood to be the angle between the contact
normal and the pressure axis and
is now understood to be the angle between the contact
normal and the pressure axis and 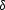 is proportional to the
difference between the uniaxial and transverse applied stresses.
Note, that for unconsolidated granular media (e.g., sand
packs) it is essential that there be some transverse confining
pressure to give the material an underlying elastic integrity (i.e.,
to prevent the vanishing of D(0)n and D(0)t). The same
assumption is required in the formalism developed by Walton (1987) and we
show here that the application of his formalism leads to results that
are identical to those derived by Schwartz (1984).
is proportional to the
difference between the uniaxial and transverse applied stresses.
Note, that for unconsolidated granular media (e.g., sand
packs) it is essential that there be some transverse confining
pressure to give the material an underlying elastic integrity (i.e.,
to prevent the vanishing of D(0)n and D(0)t). The same
assumption is required in the formalism developed by Walton (1987) and we
show here that the application of his formalism leads to results that
are identical to those derived by Schwartz (1984).
WAVES IN TRANSVERSELY ISOTROPIC ROCKS
Let x1, x2, and x3 be spatial coordinates and u1, u2,
and u3 be the displacement components of an elastic wave in a rock.
If the stress tensor is 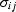 and the strain tensor is related
to the displacements by
and the strain tensor is related
to the displacements by
| 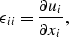 |
(3) |
and
| 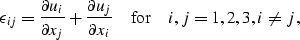 |
(4) |
then the general stress-strain relations in elastic rocks are
|  |
(5) |
where cij is the fourth rank stiffness tensor and Sijkl is the
corresponding compliance tensor. Repeated indices are summed in
(5), but not in (3). The tensor notation may
be conveniently
replaced by vectors and matrices using the Voigt notation, whereby the
subscripts of stress and strain are mapped according to the prescription
 ,
,  ,
,  ,
,  ,
, 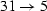 , and
, and 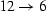 .Symmetries take care of the remaining combinations.
.Symmetries take care of the remaining combinations.
Assuming that the symmetry axis is in direction x3, so the x1x2-plane
is isotropic, then the relation between stress and strain
for such transversely isotropic media becomes
| 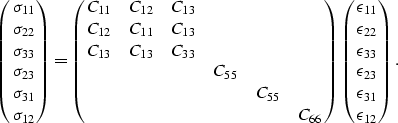 |
(6) |
A similar equation relates 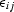 to
to 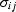 through the compliance
matrix
through the compliance
matrix 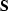 , so the stiffness matrix is just the inverse of the compliance
matrix:
, so the stiffness matrix is just the inverse of the compliance
matrix:
| 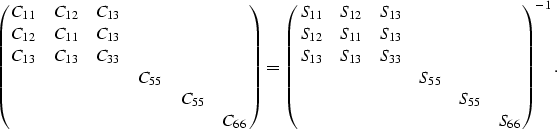 |
(7) |
For transversely isotropic materials, there are only five independent
constants, although six constants appear in each of these matrices.
The remaining condition on the constants is C11= C12+ 2C66 for the
stiffnesses, and 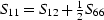 for the compliances.
These conditions follow easily from the requirement that a rotation
of the coordinate system in the x1x2-plane should not change the constants
for a transversely isotropic material.
for the compliances.
These conditions follow easily from the requirement that a rotation
of the coordinate system in the x1x2-plane should not change the constants
for a transversely isotropic material.
Taking the displacement vector  to be a plane wave proportional
to
to be a plane wave proportional
to 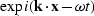 and letting
and letting 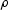 be the density
of the medium, representative characteristic dispersion relations for
propagating waves are easily shown (Berryman, 1979) to be
be the density
of the medium, representative characteristic dispersion relations for
propagating waves are easily shown (Berryman, 1979) to be
| ![\begin{eqnarray}
\rho\omega_{\pm}^2 = {\textstyle {1\over2}}\biggl\{(C_{11}+C_{5...
...}-C_{55})k_3^2\bigr]^2
+ 4(C_{13}+C_{55})^2k_1^2k_3^2}\biggr\},
\end{eqnarray}](img25.gif) |
|
| (8) |
when the polarization is normal to direction x2 (so u2 = 0),
and similarly
| 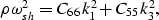 |
(9) |
when the polarization is purely normal to the direction of propagation
(so u1 = u3 = 0). Equation (8) gives two dispersion relations for
waves having mixtures of compressional and shear polarizations, being neither
pure compressional nor pure shear except in the x1 and x3 directions.
In these special directions, 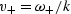 is the velocity of a pure
compressional (P) wave and
is the velocity of a pure
compressional (P) wave and 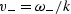 is the velocity of a pure shear (SV)
wave. For intermediate angles, these two waves are known respectively as
quasi-P and quasi-SV waves. Equation (9) is always (for all angles)
the dispersion relation for a pure shear (SH) wave.
is the velocity of a pure shear (SV)
wave. For intermediate angles, these two waves are known respectively as
quasi-P and quasi-SV waves. Equation (9) is always (for all angles)
the dispersion relation for a pure shear (SH) wave.
VELOCITY ANISOTROPY FOR GRANULAR MATERIALS
We use the results of Walton (1987) to obtain predicted stiffnesses for
a granular material comprised of a dense random packing of spheres with
constant radius under hydrostatic confining strain with an additional
uniaxial strain applied in the x3 direction. Walton gives
general expressions for elastic stiffnesses as a function of an arbitrary
applied strain. We will not quote his general expression here, but
merely write down the results we obtain from his formula using an
applied macroscopic strain of the form
| 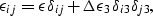 |
(10) |
where  is a uniform hydrostatic strain and
is a uniform hydrostatic strain and 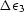 is the additional
uniaxial strain in the x3 direction. Then, introducing the
direction cosines
is the additional
uniaxial strain in the x3 direction. Then, introducing the
direction cosines 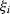 for the unit vector connecting the centers
of adjacent spheres, we find that the stiffness coefficients
depend on an average applied strain given by
for the unit vector connecting the centers
of adjacent spheres, we find that the stiffness coefficients
depend on an average applied strain given by
| 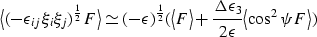 |
(11) |
where  is the average over all possible orientations of the unit
vector,
is the average over all possible orientations of the unit
vector,  is again the angle with respect to the direction of the applied
strain while F is a complicated function of direction cosines
[see Walton (1987)].
is again the angle with respect to the direction of the applied
strain while F is a complicated function of direction cosines
[see Walton (1987)].
All the formulas that follow are proportional to a constant factor of the form
| 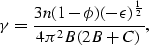 |
(12) |
where n is the average number of contacts per spherical particle, 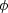 is the porosity, and
is the porosity, and
| ![\begin{eqnarray}
B = {{1}\over{4\pi}}\Biggl[{{1}\over{\mu}}+{{1}\over{\lambda+\m...
...ver{4\pi}}\Biggl[{{1}\over{\mu}}-{{1}\over{\lambda+\mu}}\Biggr],
\end{eqnarray}](img37.gif) |
(13) |
where 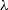 and
and 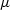 are the Lamé constants of the mineral composing
the spherical grains.
are the Lamé constants of the mineral composing
the spherical grains.
With these definitions, we find that the elastic stiffnesses are
| ![\begin{eqnarray}
C_{11}= \gamma\Biggl[{{4B}\over{3}}+{{2C}\over{5}} +
{{\Delta\e...
...\epsilon}}\biggl({{2B}\over{15}} + {{C}\over{35}}\biggr)\Biggr],
\end{eqnarray}](img40.gif) |
(14) |
| ![\begin{eqnarray}
C_{13}= \gamma\Biggl[{{2C}\over{15}}
+ {{\Delta\epsilon_3}\over{\epsilon}}\biggl({{C}\over{35}}\biggr)\Biggr],
\qquad\qquad\quad
\end{eqnarray}](img41.gif) |
(15) |
| ![\begin{eqnarray}
C_{33}= \gamma\Biggl[{{4B}\over{3}}+{{2C}\over{5}} +
{{\Delta\e...
...ver{\epsilon}}\biggl({{2B}\over{5}}+{{C}\over{7}}\biggr)\Biggr],
\end{eqnarray}](img42.gif) |
(16) |
| ![\begin{eqnarray}
C_{55}= \gamma\Biggl[{{2B}\over{3}}+{{2C}\over{15}} +
{{\Delta\...
...r{\epsilon}}\biggl({{2B}\over{15}}+{{C}\over{35}}\biggr)\Biggr],
\end{eqnarray}](img43.gif) |
(17) |
and
| ![\begin{eqnarray}
C_{66}= \gamma\Biggl[{{2B}\over{3}}+{{2C}\over{15}} +
{{\Delta\...
...r{\epsilon}}\biggl({{B}\over{15}}+{{C}\over{105}}\biggr)\Biggr].
\end{eqnarray}](img44.gif) |
(18) |
The remaining constant is given by C12= C11- 2C66. Eqs. (14)
through (18) are, in fact, the same as those derived
by Schwartz (1984) using the orientation dependent force constants
(2). To establish this correspondence, we employ the identities
| 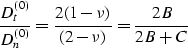 |
(19) |
and set 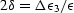 . The parameter
. The parameter  appearing in (19) is the Poisson ratio of the sphere material.
walton
appearing in (19) is the Poisson ratio of the sphere material.
walton
Figure 1
The pluses (+) and solid curve represent
experimental (Murphy, 1982)
and calculated (VP/VS)2 ratios for propagation along the pressure
axis. The (essentially) level dashed curve is the corresponding ratio
calculated for propagation in the transverse direction with the shear wave
polarized in the transverse plane. The decreasing dashed curve is
the calculated ratio for transverse propagation with shear
polarization in the axial direction.
Equations (14) through (18) can be directly employed to calculate
the three independent (VP/VS)2 ratios: C33/C55, C11/C66, and
C11/C55. In Figure 1, the results of such a calculation
are compared with experimental data on packed and well sorted (grain
diameters in the range 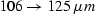 ) Ottawa sand for
the first of
these ratios. In these measurements, direct uniaxial pressure p3 was
applied to the sand pack which was subject to a nearly zero-strain
boundary condition the transverse directions. [Note that, in the isotropic
limit, these data approach the results obtained by Domenico (1977).] Because
the transverse components of the stress were not measured independently,
we cannot be certain of the relation between the applied pressure and
the parameter
) Ottawa sand for
the first of
these ratios. In these measurements, direct uniaxial pressure p3 was
applied to the sand pack which was subject to a nearly zero-strain
boundary condition the transverse directions. [Note that, in the isotropic
limit, these data approach the results obtained by Domenico (1977).] Because
the transverse components of the stress were not measured independently,
we cannot be certain of the relation between the applied pressure and
the parameter 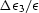 . Accordingly, we adopted the
empirical
fit
. Accordingly, we adopted the
empirical
fit 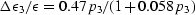 .Clearly, the agreement with the measured values is excellent and the
predicted results for the horizontally propagating modes can be
directly tested by experiment.
.Clearly, the agreement with the measured values is excellent and the
predicted results for the horizontally propagating modes can be
directly tested by experiment.
VELOCITY ANISOTROPY FROM CRACK CLOSURE
Next we consider the work of Walsh (1965a,b,c) and Nur (1969; 1971).
Originally their model was formulated in terms of crack closure in granites.
We believe, however, that models of this type can provide a phenomemological
basis for a wide variety of anisotropic rocks. Accordingly, we have
developed a version of their formalism, based on more general arguments about
relations among the compliance matrix elements for any TI material. Models of
this kind are most conveniently treated in terms of the compliance matrix.
It is therefore useful to recall the relations between the Sij
and the technical constants (Young's moduli Eii, Poisson's ratios
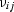 , and shear moduli
, and shear moduli 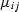 ):
):
| 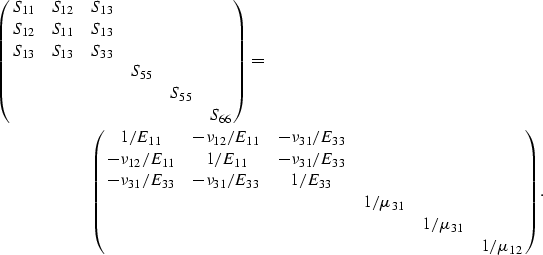 |
|
| (20) |
The basic model is that cracks are present in the rock and uniformly
distributed over angles before the application of either a hydrostatic
confining pressure or a uniaxial pressure. When pressure is applied, cracks
close if the pressure normal to the plane of a crack exceeds a threshold,
i.e., 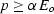 , where
, where  is the aspect ratio of the crack
and Eo is the Young's modulus of the rock with all cracks ``open.''
If a hydrostatic
pressure is applied, then the moduli change but the rock remains isotropic as
the cracks close uniformly in all directions. However, if uniaxial pressure
is applied, then those cracks oriented normal (or nearly normal) to the
symmetry axis will be closed preferentially.
is the aspect ratio of the crack
and Eo is the Young's modulus of the rock with all cracks ``open.''
If a hydrostatic
pressure is applied, then the moduli change but the rock remains isotropic as
the cracks close uniformly in all directions. However, if uniaxial pressure
is applied, then those cracks oriented normal (or nearly normal) to the
symmetry axis will be closed preferentially.
It is assumed that the cracked rock is isotropic before the application of
uniaxial pressure field 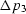 . Then, in terms
of the isotropic constants for the mineral composing the rock (without cracks)
E,
. Then, in terms
of the isotropic constants for the mineral composing the rock (without cracks)
E,  , and
, and 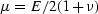 , and certain factors (in brackets) dependent
on the particular element of the compliance, the compliances are given by
, and certain factors (in brackets) dependent
on the particular element of the compliance, the compliances are given by
| ![\begin{eqnarray}
S_{11}= {{1}\over{E}}\biggl[1 + m \int N(\alpha) I_{11}(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img58.gif) |
(21) |
| ![\begin{eqnarray}
\quad S_{13}= -{{\nu}\over{E}}\biggl[1 + m \int N(\alpha) I_{13}(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img59.gif) |
(22) |
| ![\begin{eqnarray}
S_{33}= {{1}\over{E}}\biggl[1 + m \int N(\alpha) I_{33}(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img60.gif) |
(23) |
| ![\begin{eqnarray}
S_{55}= {{1}\over{\mu}}\biggl[1 + m \int N(\alpha) I_{13}(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img61.gif) |
(24) |
and
| ![\begin{eqnarray}
S_{66}= {{1}\over{\mu}}\biggl[1 + m \int N(\alpha) I_{12}(\alpha)\,d\alpha\biggr].
\end{eqnarray}](img62.gif) |
(25) |
The remaining constant is given by the rotational invariance condition
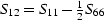 . The various new terms appearing in these equations
are
. The various new terms appearing in these equations
are 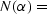 the crack aspect ratio distribution,
the crack aspect ratio distribution,
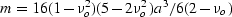 where the individual crack
volume is given by
where the individual crack
volume is given by 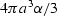 (a being the sphere radius). The other
factors in the integrands are
(a being the sphere radius). The other
factors in the integrands are
| ![\begin{eqnarray}
I_{11}(\alpha) = I_{12}(\alpha) = {{2\pi}\over{3}}
\bigl[3\cos\psi_c(\alpha)-\cos^3\psi_c(\alpha)\bigr],
\end{eqnarray}](img67.gif) |
(26) |
| 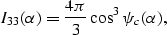 |
(27) |
where the critical angle 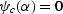 for crack closure
if
for crack closure
if 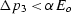 , while for larger uniaxial pressures
, while for larger uniaxial pressures
| 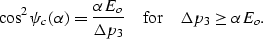 |
(28) |
The condition that 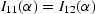 is required for transversely
isotropic media, following again from rotational symmetry of the
x1x2-plane.
Finally, we have another condition that must be fulfilled by transversely
isotropic media relating I13 to I11 and I33, i.e.,
is required for transversely
isotropic media, following again from rotational symmetry of the
x1x2-plane.
Finally, we have another condition that must be fulfilled by transversely
isotropic media relating I13 to I11 and I33, i.e.,
| ![\begin{eqnarray}
I_{13}(\alpha) = {\textstyle {1\over2}}[I_{11}(\alpha) + I_{33}(\alpha)].
\end{eqnarray}](img73.gif) |
(29) |
For values of uniaxial pressure such that 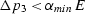 , all the
factors
, all the
factors 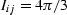 , since then the critical angle vanishes.
These equations have all the required symmetries to be those of a
transversely isotropic medium.
, since then the critical angle vanishes.
These equations have all the required symmetries to be those of a
transversely isotropic medium.
For comparison, we note that in the absence of applied pressure all
cracks are open and this model assumes the compliances all depend on the crack
aspect ratios through a common factor
| ![\begin{eqnarray}
\biggl[1 + m \int N(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img76.gif) |
(30) |
i.e., the brackets in (21)-(25) are all replaced by
(30) and, for example,
![$S_{11} = 1/E_o = (1/E)[1+m\int N\,d\alpha]$](img77.gif) .Similarly, as hydrostatic pressure is applied, the model assumes
that the rock remains isotropic as some of the cracks close. Now the
common factor is
.Similarly, as hydrostatic pressure is applied, the model assumes
that the rock remains isotropic as some of the cracks close. Now the
common factor is
| ![\begin{eqnarray}
\biggl[1 + m \int N(\alpha) \cos\psi_c(\alpha)\,d\alpha\biggr],
\end{eqnarray}](img78.gif) |
(31) |
where the critical closure angle is again given by (28).
The factor in (31) is particularly important
because identity (29) follows from the condition that an isotropic
average of the transversely isotropic results must agree with this hydrostatic
result, and so together with (27) determines (26).
walsh
Figure 2
Calculated (VP/VS)2 ratios based on the crack
closure model. The upper curve represents propagation along the pressure
axis. The middle curve is for propagation in the transverse
direction with the shear wave polarized in the transverse plane. The
lower curve is for transverse propagation with shear
polarization in the axial direction. The calculations were based on
a reasonable set of assumptions for granites: all the cracks were
taken to have aspect ratio 550.0, the porosity was 0.05, and the VP
and VS values for the rock with all cracks closed were 5.90 and
3.65 km/sec.
Illustrative calculations based on the above equations are presented
in Figure 2. Here, as in Figure 1, the same three
(VP/VS)2 ratios are displayed as a function of uniaxial stress.
Nur (1969) and Nur and Simmons (1969) have shown that, with suitably
chosen distributions 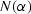 , this model provides a reasonable fit to
experimental measurements on granites. In the present context, our
objective is simply to emphasize the qualitative similarity between
the predictions of the crack closure and grain contact models.
Accordingly, the calculations shown in Figure 2 were based on a
particularly simple distribution in which all cracks were assumed to
have the same aspect ratio. The common features of Figures 1 and 2
are quite striking, particularly in light of the very different
assumptions underlying the two models.
, this model provides a reasonable fit to
experimental measurements on granites. In the present context, our
objective is simply to emphasize the qualitative similarity between
the predictions of the crack closure and grain contact models.
Accordingly, the calculations shown in Figure 2 were based on a
particularly simple distribution in which all cracks were assumed to
have the same aspect ratio. The common features of Figures 1 and 2
are quite striking, particularly in light of the very different
assumptions underlying the two models.
DISCUSSION
It has been shown by Berryman (1979) that, if the transverse isotropy is
due to fine layering, then (C11-C55)(C33-C55) -
(C13+C55)2 is always positive. This combination of stiffnesses will be
referred to as the anellipticity parameter 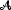 . Effective medium
calculations by Hornby et al. (1993) produce stiffness coefficients
that also exhibit a positive anellipticity parameter. The significance of
these results is that it allows us to determine, via measurements of
elastic velocities in transversely isotropic rocks, whether the
anisotropy is due to layering or due to stress. Within the grain
contact framework, we find
. Effective medium
calculations by Hornby et al. (1993) produce stiffness coefficients
that also exhibit a positive anellipticity parameter. The significance of
these results is that it allows us to determine, via measurements of
elastic velocities in transversely isotropic rocks, whether the
anisotropy is due to layering or due to stress. Within the grain
contact framework, we find
| 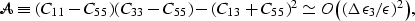 |
(32) |
showing that this characteristic quantity is small (and may vanish identically)
for finite uniaxial strains in this theory. In addition, our
numerical calculations indicate that the crack closure model also
leads to a vanishing anellipticity parameter for the simple delta function
distribution considered here. Thus it may well be true that measurements
of velocities are able to distinguish between layered (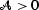 )and pressure-induced (
)and pressure-induced (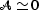 ) TI media.
Whether the accuracy of measured elastic constants will be sufficient
to distinguish these cases is uncertain at present, but this issue may be resolved
by a higher order analysis of the anellipticity parameter. In particular,
the sign of (32) is uncertain, since various terms of second and higher order
were neglected in deriving the result. It is possible that (32)
is actually negative for stress-induced anisotropy.
However, we should emphasize that
at present we do not know
of any models that consistently give a negative value for the anellipticity parameter.
) TI media.
Whether the accuracy of measured elastic constants will be sufficient
to distinguish these cases is uncertain at present, but this issue may be resolved
by a higher order analysis of the anellipticity parameter. In particular,
the sign of (32) is uncertain, since various terms of second and higher order
were neglected in deriving the result. It is possible that (32)
is actually negative for stress-induced anisotropy.
However, we should emphasize that
at present we do not know
of any models that consistently give a negative value for the anellipticity parameter.
Also of interest are Thomsen's anisotropy parameters (Thomsen, 1986)
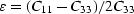 and
and ![$\delta= [(C_{13}+C_{55})^2-(C_{33}-C_{55})^2]/2C_{33}(C_{33}-C_{55})$](img85.gif) .Evaluating these parameters for the grain contact model to lowest order
in the applied uniaxial stress, we find that
.Evaluating these parameters for the grain contact model to lowest order
in the applied uniaxial stress, we find that
| ![\begin{eqnarray}
\varepsilon\simeq \delta\simeq - \biggl({{\Delta\epsilon_3}\ove...
...{35}}\biggr)/
\biggl({{2B}\over{3}}+{{C}\over{5}}\biggr)\Biggr],
\end{eqnarray}](img86.gif) |
(33) |
neglecting terms of second order in 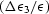 . Similarly, in
the crack closure model our numerical results indicate that
. Similarly, in
the crack closure model our numerical results indicate that 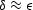 . When these two anisotropy parameters are equal,
we have the special case known as ``elliptical anisotropy.''
This fact also follows from (32),
since
. When these two anisotropy parameters are equal,
we have the special case known as ``elliptical anisotropy.''
This fact also follows from (32),
since 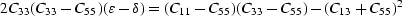 .Elliptical anisotropy occurs when the right hand side of this expression
vanishes identically. In contrast, it is known that finely layered materials
always satisfy
.Elliptical anisotropy occurs when the right hand side of this expression
vanishes identically. In contrast, it is known that finely layered materials
always satisfy 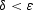 , and so have quasi-P and quasi-SV waves that are
never elliptically anisotropic. Helbig (1983) has emphasized that
finely layered TI media virtually never display elliptical anisotropy.
However, for small uniaxial stresses, the present results show that both
granular materials and systems with penny-shaped cracks exhibit
elliptical anisotropy in both the quasi-P and quasi-SV waves
(Nur and Simmons, 1969). The
significance of these results for these models of
stress induced TI behavior must be carefully evaluated.
, and so have quasi-P and quasi-SV waves that are
never elliptically anisotropic. Helbig (1983) has emphasized that
finely layered TI media virtually never display elliptical anisotropy.
However, for small uniaxial stresses, the present results show that both
granular materials and systems with penny-shaped cracks exhibit
elliptical anisotropy in both the quasi-P and quasi-SV waves
(Nur and Simmons, 1969). The
significance of these results for these models of
stress induced TI behavior must be carefully evaluated.
ACKNOWLEDGMENTS
We thank Ken Winkler for suggesting the analysis of the crack closing
model. We thank Hezhu Yin and Gary Mavko for helpful conversations about
related experiments at Stanford. We thank Brian Bonner and Pat Berge for a
number of important discussions.
REFERENCES
-
Berryman, J. G., 1979, Long-wave elastic anisotropy in transversely isotropic
media: Geophysics, 44, 896-917.
-
Domenico, S. N., 1977, Elastic properties of unconsolidated porous sand
reservoirs: Geophysics, 42, 1339-1368.
-
Helbig, K., 1983, Elliptical anisotropy -- Its significance and meaning:
Geophysics, 48, 825-832.
-
Hornby, B. E., Schwartz, L. M., and Hudson, J. A., 1993, Effective medium
modeling of the electrical and elastic properties of anisotropic
porous media, in SEG Technical Program Expanded Abstracts, Sixty-third
Annual Meeting and International Exposition, Washington, D. C.,
September 26-30, 1993, pp. 786-791.
-
Murphy, W. F., III, 1982, Effects of microstructure and pore fluids on the
acoustic properties of granular sedimentary materials,
Ph. D. Thesis, Stanford University.
-
Murphy, W. F., III, Reischer, A., and Hsu, K., 1993, Modulus
decomposition of compressional and shear velocities in sand bodies,
Geophysics, 58, 227-239.
-
Nur, A., 1969, Effects of stress and fluid inclusions on wave propagation in
rock, Ph. D. Thesis, Massachusetts Institute of Technology.
-
Nur, A., 1971, Effects of stress on velocity anisotropy in rocks with cracks:
J. Geophys. Res., 76, 2022-2034.
-
Nur, A., and Simmons, G., 1969, Stress-induced velocity anisotropy in rock:
An experimental study: J. Geophys. Res., 74, 6667-6674.
-
Schwartz, L. M., 1984, Acoustic properties of porous systems: II. Microscopic description: in Physics and Chemistry of Porous Media,
AIP Conference Proceedings, Vol. 107, D. L. Johnson and
P. N. Sen (eds.), American Institute of Physics, New York, pp. 105-118.
-
Schwartz, L. M., Johnson, D. L., and Feng, S., 1984, Vibrational modes in
granular materials: Phys. Rev. Lett., 52, 831-834.
-
Thomsen, L. M., 1986, Weak elastic anisotropy: Geophysics, 51,
1954-1966.
-
Walsh, J. B., 1965a, The effect of cracks on the compressibility of rock:
J. Geophys. Res., 70, 381-389.
-
Walsh, J. B., 1965b, The effects of cracks on the uniaxial elastic
compression of rocks: J. Geophys. Res., 70, 399-411.
-
Walsh, J. B., 1965c, The effect of cracks in rocks on Poisson's ratio:
J. Geophys. Res., 70, 5249-5257.
-
Walton, K., 1987, The effective elastic moduli of a random packing of spheres:
J. Mech. Phys. Solids, 35, 213-226.
-
Yin, H., and Nur, A., 1992, Stress-induced ultrasonic velocity and attenuation
anisotropy of rocks: in SEG Technical Program Expanded Abstracts,
Sixty-Second Annual International Meeting and Exposition, October 25-29,
1992, pp. 1073-1076.
-
Zamora, M., and Poirier, J. P., 1990, Experimental study of acoustic
anisotropy and birefringence in dry and saturated Fontainebleau sandstone:
Geophysics, 55, 1455-1465.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/15/2001
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) William F. Murphy, III,
William F. Murphy, III,![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) William F. Murphy, III,
William F. Murphy, III,![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![\begin{eqnarray}
D_n = D^{(0)}_n \left[ 1 + \delta \cos^2 \psi \right],\nonumber\\ D_t = D^{(0)}_t \left[ 1 + \delta \cos^2 \psi \right],
\end{eqnarray}](img5.gif)
![]() and the strain tensor is related
to the displacements by
and the strain tensor is related
to the displacements by
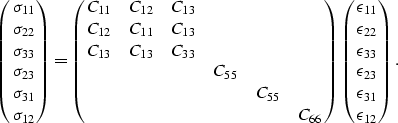
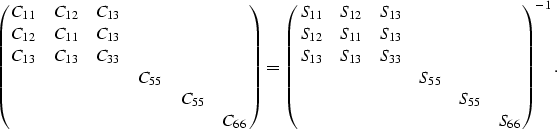
![]() to be a plane wave proportional
to
to be a plane wave proportional
to ![]() and letting
and letting ![]() be the density
of the medium, representative characteristic dispersion relations for
propagating waves are easily shown (Berryman, 1979) to be
be the density
of the medium, representative characteristic dispersion relations for
propagating waves are easily shown (Berryman, 1979) to be
![\begin{eqnarray}
\rho\omega_{\pm}^2 = {\textstyle {1\over2}}\biggl\{(C_{11}+C_{5...
...}-C_{55})k_3^2\bigr]^2
+ 4(C_{13}+C_{55})^2k_1^2k_3^2}\biggr\},
\end{eqnarray}](img25.gif)
![\begin{eqnarray}
B = {{1}\over{4\pi}}\Biggl[{{1}\over{\mu}}+{{1}\over{\lambda+\m...
...ver{4\pi}}\Biggl[{{1}\over{\mu}}-{{1}\over{\lambda+\mu}}\Biggr],
\end{eqnarray}](img37.gif)
![\begin{eqnarray}
C_{11}= \gamma\Biggl[{{4B}\over{3}}+{{2C}\over{5}} +
{{\Delta\e...
...\epsilon}}\biggl({{2B}\over{15}} + {{C}\over{35}}\biggr)\Biggr],
\end{eqnarray}](img40.gif)
![\begin{eqnarray}
C_{13}= \gamma\Biggl[{{2C}\over{15}}
+ {{\Delta\epsilon_3}\over{\epsilon}}\biggl({{C}\over{35}}\biggr)\Biggr],
\qquad\qquad\quad
\end{eqnarray}](img41.gif)
![\begin{eqnarray}
C_{33}= \gamma\Biggl[{{4B}\over{3}}+{{2C}\over{5}} +
{{\Delta\e...
...ver{\epsilon}}\biggl({{2B}\over{5}}+{{C}\over{7}}\biggr)\Biggr],
\end{eqnarray}](img42.gif)
![\begin{eqnarray}
C_{55}= \gamma\Biggl[{{2B}\over{3}}+{{2C}\over{15}} +
{{\Delta\...
...r{\epsilon}}\biggl({{2B}\over{15}}+{{C}\over{35}}\biggr)\Biggr],
\end{eqnarray}](img43.gif)
![\begin{eqnarray}
C_{66}= \gamma\Biggl[{{2B}\over{3}}+{{2C}\over{15}} +
{{\Delta\...
...r{\epsilon}}\biggl({{B}\over{15}}+{{C}\over{105}}\biggr)\Biggr].
\end{eqnarray}](img44.gif)

![]() ) Ottawa sand for
the first of
these ratios. In these measurements, direct uniaxial pressure p3 was
applied to the sand pack which was subject to a nearly zero-strain
boundary condition the transverse directions. [Note that, in the isotropic
limit, these data approach the results obtained by Domenico (1977).] Because
the transverse components of the stress were not measured independently,
we cannot be certain of the relation between the applied pressure and
the parameter
) Ottawa sand for
the first of
these ratios. In these measurements, direct uniaxial pressure p3 was
applied to the sand pack which was subject to a nearly zero-strain
boundary condition the transverse directions. [Note that, in the isotropic
limit, these data approach the results obtained by Domenico (1977).] Because
the transverse components of the stress were not measured independently,
we cannot be certain of the relation between the applied pressure and
the parameter ![]() . Accordingly, we adopted the
empirical
fit
. Accordingly, we adopted the
empirical
fit ![]() .Clearly, the agreement with the measured values is excellent and the
predicted results for the horizontally propagating modes can be
directly tested by experiment.
.Clearly, the agreement with the measured values is excellent and the
predicted results for the horizontally propagating modes can be
directly tested by experiment.
![]() , and shear moduli
, and shear moduli ![]() ):
):
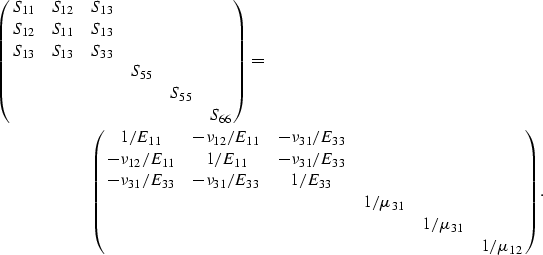
![]() , where
, where ![]() is the aspect ratio of the crack
and Eo is the Young's modulus of the rock with all cracks ``open.''
If a hydrostatic
pressure is applied, then the moduli change but the rock remains isotropic as
the cracks close uniformly in all directions. However, if uniaxial pressure
is applied, then those cracks oriented normal (or nearly normal) to the
symmetry axis will be closed preferentially.
is the aspect ratio of the crack
and Eo is the Young's modulus of the rock with all cracks ``open.''
If a hydrostatic
pressure is applied, then the moduli change but the rock remains isotropic as
the cracks close uniformly in all directions. However, if uniaxial pressure
is applied, then those cracks oriented normal (or nearly normal) to the
symmetry axis will be closed preferentially.
![]() . Then, in terms
of the isotropic constants for the mineral composing the rock (without cracks)
E,
. Then, in terms
of the isotropic constants for the mineral composing the rock (without cracks)
E, ![]() , and
, and ![]() , and certain factors (in brackets) dependent
on the particular element of the compliance, the compliances are given by
, and certain factors (in brackets) dependent
on the particular element of the compliance, the compliances are given by

![]() , this model provides a reasonable fit to
experimental measurements on granites. In the present context, our
objective is simply to emphasize the qualitative similarity between
the predictions of the crack closure and grain contact models.
Accordingly, the calculations shown in Figure 2 were based on a
particularly simple distribution in which all cracks were assumed to
have the same aspect ratio. The common features of Figures 1 and 2
are quite striking, particularly in light of the very different
assumptions underlying the two models.
, this model provides a reasonable fit to
experimental measurements on granites. In the present context, our
objective is simply to emphasize the qualitative similarity between
the predictions of the crack closure and grain contact models.
Accordingly, the calculations shown in Figure 2 were based on a
particularly simple distribution in which all cracks were assumed to
have the same aspect ratio. The common features of Figures 1 and 2
are quite striking, particularly in light of the very different
assumptions underlying the two models.
![]() . Effective medium
calculations by Hornby et al. (1993) produce stiffness coefficients
that also exhibit a positive anellipticity parameter. The significance of
these results is that it allows us to determine, via measurements of
elastic velocities in transversely isotropic rocks, whether the
anisotropy is due to layering or due to stress. Within the grain
contact framework, we find
. Effective medium
calculations by Hornby et al. (1993) produce stiffness coefficients
that also exhibit a positive anellipticity parameter. The significance of
these results is that it allows us to determine, via measurements of
elastic velocities in transversely isotropic rocks, whether the
anisotropy is due to layering or due to stress. Within the grain
contact framework, we find
![]() and
and ![]() .Evaluating these parameters for the grain contact model to lowest order
in the applied uniaxial stress, we find that
.Evaluating these parameters for the grain contact model to lowest order
in the applied uniaxial stress, we find that
![\begin{eqnarray}
\varepsilon\simeq \delta\simeq - \biggl({{\Delta\epsilon_3}\ove...
...{35}}\biggr)/
\biggl({{2B}\over{3}}+{{C}\over{5}}\biggr)\Biggr],
\end{eqnarray}](img86.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)