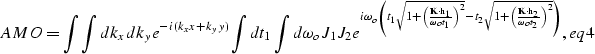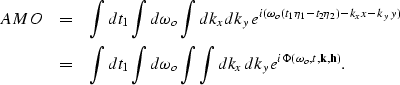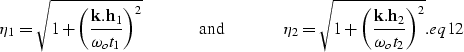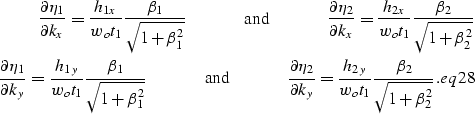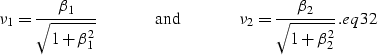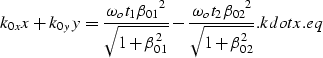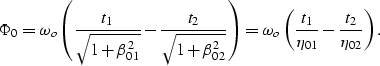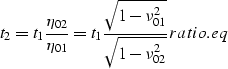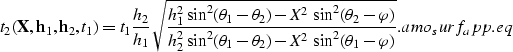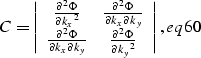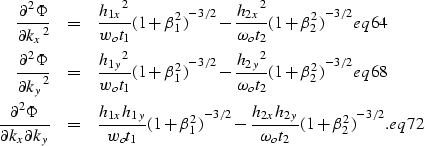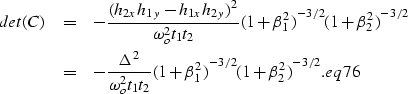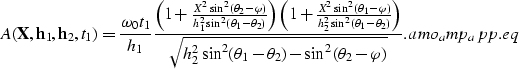![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Transformation of 3-D prestack data by Azimuth Moveout
Biondo Biondi and Nizar Chemingui
Author has no known email address
ABSTRACT
We introduce a new partial-migration operator, named Azimuth Moveout (AMO),
that rotates the azimuth and modifies the offset of 3-D prestack data.
AMO can be effectively applied to
improve the accuracy and to reduce the computational
cost of 3-D prestack imaging.
For example, a 3-D prestack dataset can be drastically reduced in size
by coherent partial-stacking after AMO.
The reduced dataset can be then imaged by prestack depth migration,
a process that would have been too expensive to apply to
the original dataset.
AMO can also be effectively used for regularizing data geometries
(e.g. correct for cable feather) and for interpolating
unevenly sampled data.
AMO is defined as the cascade of DMO and inverse DMO at
different offsets and azimuths.
We derive the time-space domain formulation of the AMO
operator by first deriving its Fourier domain representation,
and then analytically evaluating the stationary-phase approximation.
The impulse response of AMO is a surface in the time-midpoint space;
the shape of the surface is a skewed saddle, and its
spatial extent is determined by the amount
of azimuth rotation and offset continuation to be applied to the data.
When the azimuth rotation is small (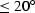 ),
the AMO operator is compact and inexpensive to apply in the
time-space domain.
We successfully tested AMO by coherently stacking traces
with similar offsets and azimuths from a synthetic land survey. ),
the AMO operator is compact and inexpensive to apply in the
time-space domain.
We successfully tested AMO by coherently stacking traces
with similar offsets and azimuths from a synthetic land survey.
|
Modern 3-D surveys, both land and marine,
have a wide range of offsets and azimuths.
Often the offset and azimuth distribution are sub-optimal because
acquisition geometry is the result of a compromise between
the maximization of data quality and practical and economic
constraints.
To optimize the imaging of 3-D datasets,
it can be useful to modify the effective
azimuth and offset distribution of the data
during processing,
without the need of a detailed a priori assumptions on the underlying
velocity function or geology.
In this paper we show that this task can be accomplished
by applying a partial migration operator that
rotates the data azimuth and changes the data absolute offset.
Because of its ability to modify the azimuth of the
data we have named this operator Azimuth Moveout (AMO).
There are many potential applications for the AMO operator.
One of the most promising, and the one that we will
illustrate with a synthetic example, is the ability to reduce the
amount of 3-D prestack data without loss of information
by coherently
stacking traces that have similar azimuths and offsets.
Because the kinematics of 3-D data are dependent
on azimuth and offsets, the data needs to be processed with
AMO prior to stacking for maximizing coherency among the
traces that are averaged.
After this data reduction,
the application of computationally
intensive processes such as 3-D prestack migration
becomes more affordable.
Another important family of applications is the regularization
of data geometries;
e.g. the correction for cable feather in marine surveys.
After this correction the data can be processed with
more efficient algorithms, either because the survey is closer to
fulfill 2-D assumptions, or because
efficient methods are available for imaging single-azimuth data
().
Finally, we believe that AMO can be effectively employed
for ``wave-equation'' interpolation of 3-D data
()
in order to overcome spatial aliasing problems or, more simply,
to correct for uneven coverage ().
The AMO operator can be defined as the cascade of an imaging operator
that acts on data with a given offset and azimuth, followed
by a forward modeling operator that reconstructs the data
at a different offset and azimuth.
Any 3-D prestack imaging operator can be used for defining AMO.
However, the characteristics of the resulting AMO operator,
such as accuracy, cost and degree
of required a-priori knowledge of the velocity function,
will depend on the choice of the 3-D prestack operator
used for its definition.
For example, if 3-D prestack depth migration were used
to define AMO, the resulting AMO operator would be very accurate.
But, on the other hand, it
would require a detailed knowledge of the velocity function,
and it would be very difficult to derive its analytical
representation leading to a potentially expensive implementation.
Because of these considerations we have chosen to define AMO from
constant-velocity dip moveout (, ).
We selected DMO for two main reasons.
First, DMO is velocity independent, within the
well understood limitations of a constant velocity assumption,
since it is applied to the data after NMO,
which removes the first order effects of velocity variations.
Second DMO can be formulated as acting on data with constant
offset and azimuth, and thus it naturally lends
itself to a straightforward derivation of AMO.
Because we derived AMO from DMO, AMO has potentially similar
strengths and weaknesses as DMO has.
However, we speculate that AMO can be effectively applied when
velocity variations are too strong for DMO to successfully
continue the data all the way to zero offset.
The rationale of this claim, that must be substantiated
by further analysis and results, is that
the AMO transformation is correct to the first order.
Therefore, if AMO is applied
when the azimuth rotation and offset continuation
are small it should be fairly accurate.
However, a generalization
of AMO to variable velocity DMO
(, , , )
is likely to be more accurate than the AMO operator presented in this paper.
For some applications, such as the synthesis of 2-D lines from 3-D data,
AMO is related to the two-pass 3-D migration
proposed by Canning and Gardner ,
which is based on the successive application of DMO and inverse DMO.
However, AMO can be applied to a wider set of problems and datasets
because the geometry of the output data is arbitrary.
In addition to data regularization,
AMO can be applied to data reduction and interpolation.
Furthermore, the application of AMO as a single-step procedure
can achieve substantial computational savings
by exploiting the reduced size of the AMO operator when
azimuth rotation and offset continuation are small.
In the next section we will derive the AMO operator
starting from the Fourier domain formulation of DMO ()
and inverse DMO ().
However, because AMO is intented to be applied to unevenly
sampled data a Fourier domain formulation is of
little practical interest. Therefore, we derived
a time-space formulation of the AMO operator by applying
the stationary-phase method to its Fourier expression.
The impulse response of the time-space AMO
is a skewed saddle surface. The spatial extent of the operator
increases with the amount of azimuth rotation and offset
continuation that are applied to the data.
When the azimuth rotation and offset
continuation are small the AMO operator is very compact,
and thus is relatively inexpensive to apply as an integral operator.
AZIMUTH MOVEOUT OPERATOR
We define AMO as an operator that transforms 3-D prestack data
with a given offset and azimuth to equivalent data
with a different offsets and azimuths.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
a graphical representation of this offset transformation;
the input data with offset
shows
a graphical representation of this offset transformation;
the input data with offset
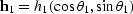 is transformed into data with offset
is transformed into data with offset
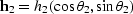 .AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator,
and, since 3-D prestack data is often irregularly sampled,
it is most conveniently applied as
an integral operator in the time-space domain.
For this purpose, in this section we derive
a time-space representation of the AMO operator.
We first derive the AMO operator starting from the classical
definition of DMO in the frequency-wavenumber domain
()
and the definition of its inverse
().
We then evaluate the stationary-phase approximation of
the AMO operator expressed in the frequency-wavenumber domain.
The stationary-phase approximation yields a time-space representation
of the AMO operator that can be applied
as an integral operator.
Although, integral AMO can be applied to irregularly sampled data,
an accurate implementation of AMO
must avoid aliasing of the data and of the operator.
sketchwidth=4.2inNR
Map view of offset and azimuth of AMO input and output traces.
.AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator,
and, since 3-D prestack data is often irregularly sampled,
it is most conveniently applied as
an integral operator in the time-space domain.
For this purpose, in this section we derive
a time-space representation of the AMO operator.
We first derive the AMO operator starting from the classical
definition of DMO in the frequency-wavenumber domain
()
and the definition of its inverse
().
We then evaluate the stationary-phase approximation of
the AMO operator expressed in the frequency-wavenumber domain.
The stationary-phase approximation yields a time-space representation
of the AMO operator that can be applied
as an integral operator.
Although, integral AMO can be applied to irregularly sampled data,
an accurate implementation of AMO
must avoid aliasing of the data and of the operator.
sketchwidth=4.2inNR
Map view of offset and azimuth of AMO input and output traces.
The DMO operator and its inverse, DMO-1, can be
defined in the zero-offset frequency 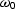 and midpoint wavenumber
and midpoint wavenumber 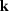 as
as
| 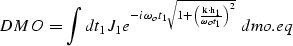 |
(1) |
| 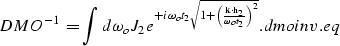 |
(2) |
The traveltimes t1 and t2 are respectively the
traveltime of the input data after NMO, and the traveltime of the
results before applying inverse NMO.
The Jacobians in expressions dmo.eq and dmoinv.eq
can be either the ones proposed in the original Hale's formulation
or the improved ones proposed by Zhang .
The AMO operator is given by the cascades
of DMO and DMO-1 and can be written as
| 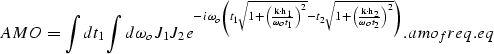 |
(3) |
The derivation of the stationary-phase approximation of the
AMO operator is fairly lengthy and complex.
We present the outline of this derivation in Appendix A.
The equation for the kinematics of the impulse response
is,
| 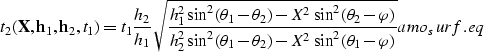 |
(4) |
while the amplitudes, when Zhang's Jacobian is used,
are given by
| 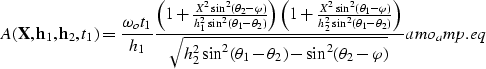 |
(5) |
where 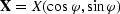 is the output location
vector in
midpoint coordinates.
Notice that the zero-offset frequency
is the output location
vector in
midpoint coordinates.
Notice that the zero-offset frequency 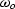 enters
as multiplicative factor in the expression for AMO amplitudes,
but the data is never available as zero-offset data during the AMO
process. The effect of this multiplicative factor can be approximated
by a time-domain filter applied either to the input or to the
output data.
For given input half-offset and time (
enters
as multiplicative factor in the expression for AMO amplitudes,
but the data is never available as zero-offset data during the AMO
process. The effect of this multiplicative factor can be approximated
by a time-domain filter applied either to the input or to the
output data.
For given input half-offset and time (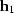 , t1) and
output half-offset
, t1) and
output half-offset 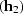 ,equations amo_surf.eq and amo_amp.eq
define a surface in the time-midpoint space.
The surface is a skewed saddle; its shape and spatial extent
are controlled by the values of the absolute offsets
and by the azimuth rotation, i.e.;
the differences in azimuths between the input and the output data.
Consistent with intuition, the spatial extent of the
operator has a maximum for rotation of 90 degrees and vanishes
when offsets and azimuth rotation tend to zero.
Furthermore, it can be easily verified that t2= t1 for
the zero-dip components of the data; that is,
the kinematics of zero-dip data after NMO do not depend on azimuth
and offset.
Figure
,equations amo_surf.eq and amo_amp.eq
define a surface in the time-midpoint space.
The surface is a skewed saddle; its shape and spatial extent
are controlled by the values of the absolute offsets
and by the azimuth rotation, i.e.;
the differences in azimuths between the input and the output data.
Consistent with intuition, the spatial extent of the
operator has a maximum for rotation of 90 degrees and vanishes
when offsets and azimuth rotation tend to zero.
Furthermore, it can be easily verified that t2= t1 for
the zero-dip components of the data; that is,
the kinematics of zero-dip data after NMO do not depend on azimuth
and offset.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the AMO impulse response for h2= h1=1 km
and azimuth rotation of 30 degrees.
The amplitudes of the operator are gray-coded on the surface.
The darker the surface, the higher the amplitudes.
The rendering of the surface was cutoff for amplitudes
lower than 10% of the maximum.
Figure
shows the AMO impulse response for h2= h1=1 km
and azimuth rotation of 30 degrees.
The amplitudes of the operator are gray-coded on the surface.
The darker the surface, the higher the amplitudes.
The rendering of the surface was cutoff for amplitudes
lower than 10% of the maximum.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the AMO impulse response for the same values
of the absolute offsets as for Figure
shows the AMO impulse response for the same values
of the absolute offsets as for Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
but azimuth rotation of only 10 degrees.
As expected, for smaller azimuth rotations
the AMO operator becomes much narrower, and the
skew of the saddle decreases.
amo-win-30-5width=4.0inNR
3-D rendering of AMO impulse response for
half-offset equal to 1 Km and azimuth rotation
equal to
,
but azimuth rotation of only 10 degrees.
As expected, for smaller azimuth rotations
the AMO operator becomes much narrower, and the
skew of the saddle decreases.
amo-win-30-5width=4.0inNR
3-D rendering of AMO impulse response for
half-offset equal to 1 Km and azimuth rotation
equal to 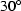 .amo-win-10-5width=4.0inNR
3-D rendering of AMO impulse response for
half-offset equal to 1 Km and azimuth rotation
equal to
.amo-win-10-5width=4.0inNR
3-D rendering of AMO impulse response for
half-offset equal to 1 Km and azimuth rotation
equal to 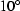 .
.
Notice that the expression for the AMO surface
is not valid when either h1 or h2 are set to zero,
or when the azimuth rotation is set to zero.
This is not surprising, because in these cases the operator
changes from being a surface to be a line.
This change in the dimensionality of the operator causes
the stationary-phase solution to become singular.
However, a different stationary-phase approximation
can be derived for these special cases, and the
expression of the traveltime curve is then given by the
following solutions of a quadric equation
| ![\begin{eqnarray}
\lefteqn{t_2(X,h_1,h_2,t_1)=} \nonumber \\ & {t}_{1}\frac{\sqrt...
...^2-X^2]}}}{\sqrt{2}h_2} & h_{2}\geq h_{1}.
\EQNLABEL{same_azim.eq}\end{eqnarray}](img17.gif) |
|
| |
| (6) |
The width of the operator defined in equation same_azim.eq
is equal to the difference between the input and output
offsets.
As expected, the expression reduces to the known expression
for integral DMO when the output
half-offset h2 is set to zero and
to inverse DMO when input half-offset h1 is set to zero.
Incidentally, equation same_azim.eq defines
an operator for offset-continuation of 2-D prestack data,
and it can have useful applications by its own.
COHERENT PARTIAL STACKING OF A SYNTHETIC
3-D LAND DATASET
AMO can be applied to reduce the data
size of a 3-D prestack dataset by coherently stacking traces
with similar absolute offsets and azimuths.
For example, a land dataset with a wide range of azimuths
and offsets can be reduced to a small set of data-cubes
with constant offset and azimuth.
Then, each of these common-offset cubes can be migrated
independently with a 3-D prestack depth migration.
The migrated cubes can be stacked together to form the
final image, or analyzed to refine the velocity model.
To test the application of AMO to this data
reduction procedure, we have created a synthetic dataset
``recorded'' with an idealized land acquisition geometry.
The geophones were distributed on a set of parallel lines,
and the shots were positioned along lines perpendicular to the geophone
lines.
The shot and geophone axes were uniformly sampled for achieving equal
offset and azimuth distribution for all the midpoints
in the central area of the survey.
We opted for a regular coverage to analyze
the properties of the AMO operator and of our integral
implementation in a simple case.
But AMO does not require regular geometry; it can actually
be used for regularizing data geometries.
We modeled the data by a simple Kirchhoff algorithm
assuming constant velocity of 2 km/s
and a single point diffractor at a depth of 200 meters.
The constant velocity assumption was again for the
sake of simplicity;
tests with a more complex velocity function are required.
From this dataset we synthesized a data cube with one single
offset (650 m) and one single azimuth (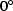 )by applying AMO to all the traces with offset
within the (600 m, 700 m) interval
and azimuth within the (
)by applying AMO to all the traces with offset
within the (600 m, 700 m) interval
and azimuth within the (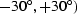 interval.
The total number of input traces processed with AMO was about 320,000,
and the output cube was made of about 16,000 traces;
the reduction factor thus was about 20.
Figure
interval.
The total number of input traces processed with AMO was about 320,000,
and the output cube was made of about 16,000 traces;
the reduction factor thus was about 20.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the absolute offset and azimuth distribution
for the input traces that were processed by AMO.
OAwidth=4.inCR
Absolute offsets and azimuths of input-data traces processed by AMO.
Consistently with the theory, AMO was applied after NMO,
and inverse NMO was applied after AMO.
To check the results of AMO processing we also
generated a reference dataset with absolute offset equal to
650 meters and azimuth equal to zero degrees.
For comparison, we also computed the result of stacking
the same traces after NMO without applying AMO.
Figure
shows the absolute offset and azimuth distribution
for the input traces that were processed by AMO.
OAwidth=4.inCR
Absolute offsets and azimuths of input-data traces processed by AMO.
Consistently with the theory, AMO was applied after NMO,
and inverse NMO was applied after AMO.
To check the results of AMO processing we also
generated a reference dataset with absolute offset equal to
650 meters and azimuth equal to zero degrees.
For comparison, we also computed the result of stacking
the same traces after NMO without applying AMO.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows time-slices taken from these three datasets
at a constant time of .96 seconds.
Between the result of AMO (Figure
shows time-slices taken from these three datasets
at a constant time of .96 seconds.
Between the result of AMO (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b) and
the reference dataset (Figure
b) and
the reference dataset (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a)
there are few differences in the frequency content and amplitudes.
The AMO results also show artifacts inside the elliptical diffraction curve,
but overall, AMO has been successful in reconstructing the prestack data.
In contrast, the simple uncoherent stacking process (Figure
a)
there are few differences in the frequency content and amplitudes.
The AMO results also show artifacts inside the elliptical diffraction curve,
but overall, AMO has been successful in reconstructing the prestack data.
In contrast, the simple uncoherent stacking process (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c)
failed to reconstruct the data.
The data have lost coherency and, even where the
data did stack coherently, the kinematics are wrong.
The error in kinematics is larger for the data components
dipping along the zero azimuth direction and vanishes
along the 90 degree azimuth.
The most likely explanation of the artifacts in the AMO results
is that our implementation of integral
AMO needs a few improvements.
Areas that need improvement are the anti-aliasing operator
and the transition between the 3-D AMO of equation amo_surf.eq
and the 2-D AMO operator of equation same_azim.eq.
c)
failed to reconstruct the data.
The data have lost coherency and, even where the
data did stack coherently, the kinematics are wrong.
The error in kinematics is larger for the data components
dipping along the zero azimuth direction and vanishes
along the 90 degree azimuth.
The most likely explanation of the artifacts in the AMO results
is that our implementation of integral
AMO needs a few improvements.
Areas that need improvement are the anti-aliasing operator
and the transition between the 3-D AMO of equation amo_surf.eq
and the 2-D AMO operator of equation same_azim.eq.
To gain a better insight into the properties
of the AMO operator we show the same three datasets
sliced along different directions.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the vertical slices taken along
the in-line direction.
The artifacts of the AMO results are clearly visible as well as
the inaccuracies in amplitude along
the top of the diffraction curve (Figure
shows the vertical slices taken along
the in-line direction.
The artifacts of the AMO results are clearly visible as well as
the inaccuracies in amplitude along
the top of the diffraction curve (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b).
The kinematics of the result of uncoherent stacking (Figure
b).
The kinematics of the result of uncoherent stacking (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c)
are wrong, except for the zero-dip component of the data.
Figure
c)
are wrong, except for the zero-dip component of the data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the vertical slices taken along
the cross-line direction. The kinematics of all three results are
similar, though the amplitudes of uncoherent stacking (Figure
shows the vertical slices taken along
the cross-line direction. The kinematics of all three results are
similar, though the amplitudes of uncoherent stacking (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c)
decrease too rapidly with dips.
Finally, Figure
c)
decrease too rapidly with dips.
Finally, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the vertical slices taken along
the direction at an angle of 45 degrees with respect to the axis.
Uncoherent stacking (Figure
shows the vertical slices taken along
the direction at an angle of 45 degrees with respect to the axis.
Uncoherent stacking (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c) totally
destroyed the data, except
for the the zero-dip components.
c) totally
destroyed the data, except
for the the zero-dip components.
CONCLUSIONS
The effective offset and azimuth of 3-D prestack data can be
modified during the processing flow by
applying a partial migration operator (AMO) to the prestack data.
We defined the AMO operator in the Fourier domain
as the cascade of DMO and inverse DMO.
The time-space representation of the AMO
operator is then derived by
analytically evaluating the stationary-phase
approximation of its Fourier representation.
The application of AMO in one single step
instead of two steps (DMO followed by inverse DMO)
leads to substantial computational savings.
The AMO operator is compact in space when the azimuth rotation and
offset continuation applied to the data are small.
By applying AMO we successfully reduced the data size by a factor of
20 for a synthetic 3-D land survey by performing a coherent partial stack
of traces with similar offsets and azimuths.
We synthesized a constant offset and
azimuth cube from traces with offset varying by up 100 meters
and azimuth varying by up 60 degrees.
Discussions with Dave Nichols, David Lumley, and François Audebert
have helped to clarify the concept of AMO.
[SEP,amo]
Comp-twidth=6.5inCR
Time-slices
taken from: a) the reference dataset, b) the AMO results,
and c) the uncoherent stacking results.
Comp-ywidth=6.5inCR
In-line slices
taken from: a) the reference dataset, b) the AMO results,
and c) the uncoherent stacking results.
Comp-xwidth=6.5inCR
Cross-line slices
taken from: a) the reference dataset, b) the AMO results,
and c) the uncoherent stacking results.
Comp-diagwidth=6.5inCR
Diagonal slices
taken from: a) the reference dataset, b) the AMO results,
and c) the uncoherent stacking results.
A
STATIONARY-PHASE EVALUATION OF AMO INTEGRAL
This appendix describes the application of the stationary phase method to
approximate the 3-D AMO kernel in the time-space domain.
Our derivation has a similar flavor to the stationary-phase approximation
of the conventional DMO operator presented in ().
From equation amo_freq.eq in the main text, we can write
the AMO operator in the time-space domain as
| 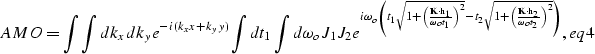 |
(7) |
where 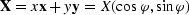 is the
output location vector in midpoint coordinates;
for sake of notation simplicity we assume that
the impulse response is centered at the origin of the midpoint coordinates.
We seek to find an approximate solution for the
is the
output location vector in midpoint coordinates;
for sake of notation simplicity we assume that
the impulse response is centered at the origin of the midpoint coordinates.
We seek to find an approximate solution for the 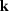 integral. We begin
by rewriting eq4 as
integral. We begin
by rewriting eq4 as
| 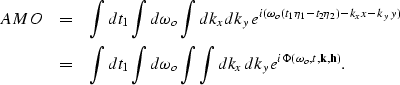 |
|
| (8) |
The phase of this integral is,
| 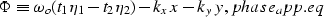 |
(9) |
where,
| 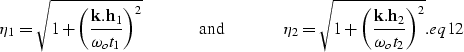 |
(10) |
Next we make the following change of variables and let,
| 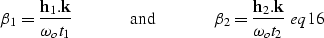 |
(11) |
therefore, 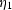 and
and 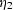 become
become
| 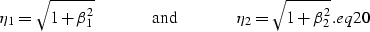 |
(12) |
The derivatives of  and
and  with respect to the
wavenumbers kx and ky can be written as
with respect to the
wavenumbers kx and ky can be written as
| 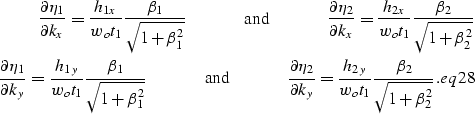 |
|
| (13) |
Making one more change of variables, we let
| 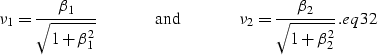 |
(14) |
Setting the derivative of the phase 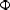 to zero yields the system
of equations:
to zero yields the system
of equations:
| 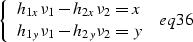 |
(15) |
which we solve for 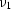 and
and 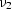 (i.e.,
(i.e., 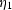 and
and 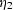 )
at the stationary
path
)
at the stationary
path 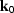 . The determinant of the system is given by
. The determinant of the system is given by
| 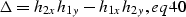 |
(16) |
and the solutions for 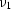 and
and 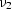 are
are
| 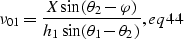 |
(17) |
and
| 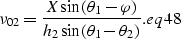 |
(18) |
Now we need to evaluate the phase function  along
the stationary path
along
the stationary path  .By respectively multiplying the equations in eq36 by
k0x and k0y and summing them together we obtain,
.By respectively multiplying the equations in eq36 by
k0x and k0y and summing them together we obtain,
| 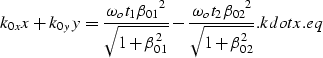 |
(19) |
Substituting this relationship into the expression of the phase
function [equation phase_app.eq] we obtain
| 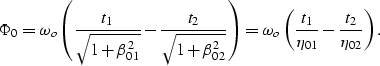 |
(20) |
The phase function along the stationary path is thus
peaked for
| 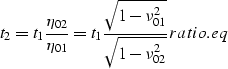 |
(21) |
Substituting equations eq44 and eq48
into ratio.eq we obtain amo_surf.eq
of the main text;
| 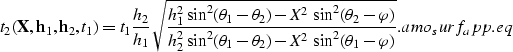 |
(22) |
Next we will derive an expression for the amplitudes of the AMO
impulse response.
The stationary-phase approximation for the amplitudes
of the 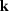 integral in equation eq4 is ()
integral in equation eq4 is ()
| 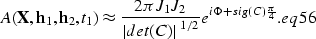 |
(23) |
Therefore we need to evaluate the determinant and the signature
of the curvature matrix C, defined as
| 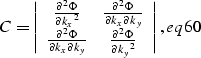 |
(24) |
whereas the signature sig(C) is given by the number of
positive eigenvalues minus the number of negative eigenvalues.
Taking the second order partial derivatives of  with respect to kx and
ky and using the definitions of
with respect to kx and
ky and using the definitions of  and
and 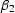 yields the expressions for
yields the expressions for
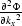 ,
, 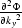 and
and 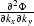 :
:
| 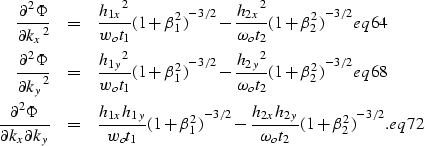 |
(25) |
| (26) |
| (27) |
With a little algebra one may verify that the determinant of the curvature
matrix is
| 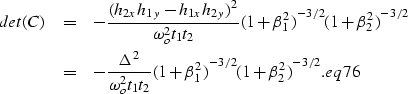 |
|
| (28) |
We notice that the determinant of C is always negative. Given that the
determinant is the product of eigenvalues and C is a two by two matrix, thus
C has two eigenvalues which have opposite signs and therefore the signature
of C is null.
Using Zhang's (1988) Jacobian, we compute the amplitudes along the surface
defined by equation amo_surf_app.eq
that gives the dynamics of the impulse response
[equation amo_amp.eq in the main text];
| 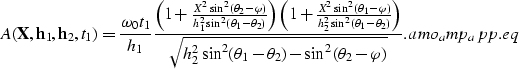 |
(29) |
2-D AMO operator
When the input offset h1 is parallel to
the output offset h2
the determinant [equation eq40] of the system eq36
is equal to zero.
In this case, as we discussed in the main text,
the 3-D AMO operator degenerates into a 2-D operator.
The fact that the determinant of the system of equations
is equal to zero means that the two equations are linearly dependent,
and that we are left with only one equation.
However, because the operator is two-dimensional,
the number of components of the unknown 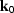 also goes from two to one.
Consequently, another stationary phase approximation
to the AMO operator can be found.
The new equation is a quartic, and
unfortunately, we have not been able to solve this
new equation analytically yet.
However, we have found the solution for
the kinematics of the operator with the help of Mathematica;
the resulting expression for the 2-D AMO operator is
presented in equation same_azim.eq of the main text.
also goes from two to one.
Consequently, another stationary phase approximation
to the AMO operator can be found.
The new equation is a quartic, and
unfortunately, we have not been able to solve this
new equation analytically yet.
However, we have found the solution for
the kinematics of the operator with the help of Mathematica;
the resulting expression for the 2-D AMO operator is
presented in equation same_azim.eq of the main text.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/15/2001
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
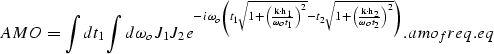
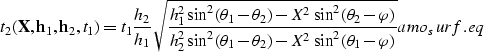
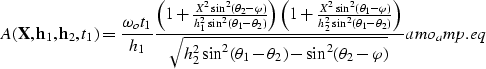
![\begin{eqnarray}
\lefteqn{t_2(X,h_1,h_2,t_1)=} \nonumber \\ & {t}_{1}\frac{\sqrt...
...^2-X^2]}}}{\sqrt{2}h_2} & h_{2}\geq h_{1}.
\EQNLABEL{same_azim.eq}\end{eqnarray}](img17.gif)