![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTIn principle, downward continuation of 3-D prestack data should be carried out in a 5-D computational space, even when the dataset to be migrated is only 3-D or 4-D. Unless this efficiency issue is solved, 3-D prestack migration methods based on the solution of the one-way wave equation are uncompetitive with Kirchhoff methods. We present a method for downward continuing common-azimuth data in the frequency-wavenumber domain in the original 4-D space of the common-azimuth data geometry. The method is based on a stationary-phase approximation of the one-way wave equation and can be applied to both phase-shift and Stolt migrations. The proposed migration methods are exact for constant velocity, and approximate for velocity varying with depth. However, results of some numerical experiments on synthetic data show that the approximation is good even in presence of strong vertical velocity gradients. |
As computational power of scientific computers keeps growing, 3-D prestack migration is becoming within the reach of the seismic industry. For 3-D prestack migration Kirchhoff methods are often preferred over methods based on the recursive downward continuation of the recorded wavefield because of their flexibility in handling 3-D prestack data geometries (). Kirchhoff methods can be employed to efficiently migrate datasets with uneven spatial sampling and datasets that are subsets of the complete prestack data, such as common-offset cubes and common-azimuth cubes. For recursive methods the irregular sampling problem can be addressed with an interpolation preprocessing step, though in practice it can be a challenging task. However, in principle the downward continuation of prestack subsets should be carried out in the full 5-D data space, even when the original subset is 3-D (common offset) or 4-D (common azimuth). As a result of these constraints most of the computations are wasted on propagating components of the wavefield that are either equal to zero or do not contribute to the final image. These potential limitations of recursive methods have led the industry to pursue almost exclusively Kirchhoff methods for 3-D prestack migration (, ), though recursive methods have some intrinsic advantages over Kirchhoff methods. First, they are potentially more accurate and robust because they are based on the full wave-equation and not an asymptotic solution based on ray theory. Second, when they can be used to extrapolate the recorded data without increasing their dimensionality (e.g. zero-offset data), they can be implemented more efficiently than the corresponding Kirchhoff methods.
In this paper we develop a method for efficiently imaging common-azimuth data by downward continuing the data in the original 4-D space. An efficient algorithm for migrating common-azimuth subsets has useful practical applications because common-azimuth data are either the result of a collection of actual physical experiments (e.g. single-streamer marine survey with negligible cable feather) or they may be synthesized by preprocessing (). Our method is potentially very efficient for migrating common-azimuth data but it is exact (within the limitations of a stationary phase approximation (), as we will discuss in the following section) only for the simple case of constant propagation velocity. For the case of velocity varying with depth we propose a simple and efficient approximation and we explore the range of validity of our approximation by analyzing the results of some simple numerical experiments. But more studies are required to determine its accuracy in the more complex, and interesting, case of velocity being a general function of the spatial coordinates.
An important application of our method that is unaffected by the constant velocity assumption is the efficient computation of migration velocity scans from common-azimuth data by a Stolt migration (). A 3-D time-migrated image can be extracted from these multiple-velocity migrations with a similar procedure to the one that is routinely applied to 2-D data. Furthermore, these migration velocity scans can also be effective tools for estimating the velocity function (, ).
COMMON-AZIMUTH PHASE-SHIFT MIGRATION
3-D prestack data can be downward continued in the frequency-wavenumber
domain by applying the 3-D double square root equation (DSQR).
In 3-D the DSQR equation is function of five scalar variables:
the temporal frequency (![]() ),
the two components of the midpoint wavenumber
vector
),
the two components of the midpoint wavenumber
vector ![]() ),
and the two components of the offset wavenumber
vector
),
and the two components of the offset wavenumber
vector ![]() ).
Therefore, in the general case the dimensionality of
the computational domain is five.
However, the data is not always 5-D but it is often 3-D or 4-D.
When the dimensionality of the data is lower
than five it would be more efficient to use an algorithm that
downward continues the data in less than 5 dimensions,
if such an algorithm were available.
Common-azimuth data has only four dimensions because
the offset vectors between source and receivers are constrained to
have the same azimuth.
The four axis are: recording time, two midpoints,
and the offset along the azimuthal direction.
A phase-shift migration of common-azimuth data in a 4-D computational
space can be derived
by evaluating the stationary-phase approximation
of the full 3-D DSQR equation (Appendix A).
The resulting expression is
).
Therefore, in the general case the dimensionality of
the computational domain is five.
However, the data is not always 5-D but it is often 3-D or 4-D.
When the dimensionality of the data is lower
than five it would be more efficient to use an algorithm that
downward continues the data in less than 5 dimensions,
if such an algorithm were available.
Common-azimuth data has only four dimensions because
the offset vectors between source and receivers are constrained to
have the same azimuth.
The four axis are: recording time, two midpoints,
and the offset along the azimuthal direction.
A phase-shift migration of common-azimuth data in a 4-D computational
space can be derived
by evaluating the stationary-phase approximation
of the full 3-D DSQR equation (Appendix A).
The resulting expression is
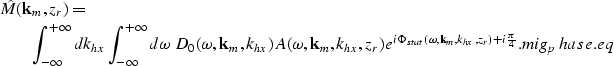 |
||
| (1) |
| (2) |
![\begin{eqnarray}
\lefteqn{DSQR(\omega,{\bf k}_{m},{\bf k}_{h},z^{'})=} \nonumber...
...(k_{mx}-k_{hx}\right)^2 + \left(k_{my}-k_{hy}\right)^2 ]} \right\}\end{eqnarray}](img9.gif) |
||
| (3) |
When the velocity is constant (v(z')=V) the global stationary path is independent of the reflector depth zr and it can be derived analytically as equal to
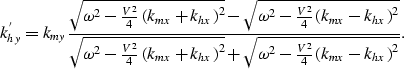 |
(4) |
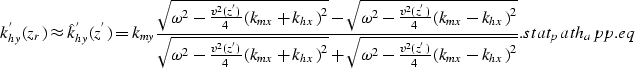 |
(5) |
In principle the proposed method could be generalized to handle lateral velocity variations by using the Phase Shift Plus Interpolation () methodology. However, we think that a better understanding of the implications of the approximation introduced in equation stat_path_app.eq is required before we apply the method to more general cases.
COMMON-AZIMUTH STOLT MIGRATION In the previous section we have introduced an efficient phase-shift migration algorithm for common-azimuth datasets. Because for constant velocity Stolt migration algorithms are more efficient than phase-shift ones, we will now derive an algorithm for common-azimuth Stolt migration. Probably the most promising application of this new 3-D Stolt migration is the computation of constant migration velocity scans. As it is routinely done for 2-D prestack Stolt, this multiple-velocity migrations can be used for extracting a time-migrated image and for estimating the velocity function in a dip-independent fashion.
The fundamental result of our development is the derivation of a new Stolt change of variables to be applied to common-azimuth data in the frequency-wavenumber domain. As we show in Appendix B, the new change of variables can be recast in a way that shows how in constant velocity, 3-D prestack migration can be seen as the cascade of two processes: 2-D prestack migration along the azimuth direction, and poststack migration along the cross-azimuth direction. Canning and Gardner showed a similar result, however in their two-pass migration the poststack migration along the cross-azimuth direction comes before the 2-D prestack migration. The migration of a common-azimuth dataset can be expressed as
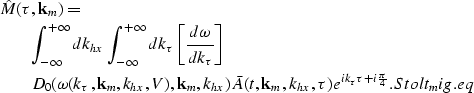 |
||
| (6) |
After lengthy algebraic manipulations the dispersion
relation ![]() can be recast as the cascade of two
changes of variable:
the first is the change of variable
for 2-D prestack Stolt migration, i.e.;
can be recast as the cascade of two
changes of variable:
the first is the change of variable
for 2-D prestack Stolt migration, i.e.;
| (7) |
| (8) |
This result has a simple intuitive explanation in terms of what is known about the kinematics of two-pass 3-D poststack migration () and 3-D DMO (). The outline of the reasoning is the following: first we consider that constant velocity 3-D poststack migration can be split along two perpendicular directions (azimuth and cross-azimuth in our case) without loss of accuracy. Second, we consider that for constant velocity 3-D DMO is kinematically exact and reduces to 2-D DMO along the azimuthal direction. Consequently, constant velocity prestack migration of common-azimuth data can be achieved by cascading NMO+DMO with poststack migration along the azimuth direction followed by poststack migration along the cross-azimuth direction. Finally we recognize that the first two steps of this procedure are equivalent to 2-D prestack migration along the azimuthal direction.
Though the dispersion relation ![]() is more meaningfully
described as the cascade of the two transformations expressed
in equations clpres.eq and clpos.eq
the regridding of the data can be accomplished
in one single step.
Consequently, if the additional costs of performing FFT along the
cross-azimuth midpoint axis and of handling the
large amount of data are neglected,
the proposed 3-D prestack Stolt migration
of a set of parallel lines with a common-azimuth is comparable
to the cost of migrating the same lines with a conventional
2-D prestack Stolt migration algorithm.
is more meaningfully
described as the cascade of the two transformations expressed
in equations clpres.eq and clpos.eq
the regridding of the data can be accomplished
in one single step.
Consequently, if the additional costs of performing FFT along the
cross-azimuth midpoint axis and of handling the
large amount of data are neglected,
the proposed 3-D prestack Stolt migration
of a set of parallel lines with a common-azimuth is comparable
to the cost of migrating the same lines with a conventional
2-D prestack Stolt migration algorithm.
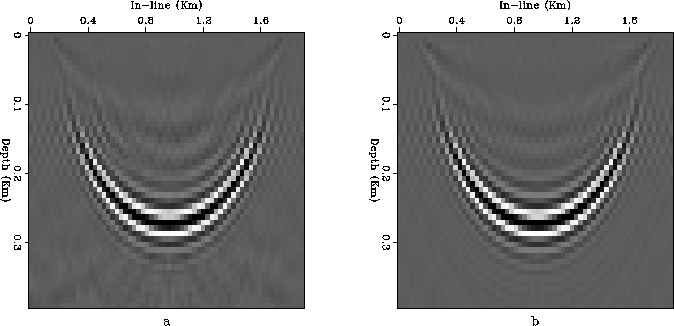
NUMERICAL RESULTS To check the validity of the proposed migration methods and to explore their limits of applicability, we migrated a common-azimuth dataset containing a band limited impulse. As a benchmark for judging the quality of the results obtained using the proposed common-azimuth Stolt and phase-shift migrations, we use the results of applying phase-shift migration to a full 5-D prestack data, thus without any stationary-phase approximation.
First we will analyze the results of both the new migration methods
in a medium with constant velocity of 2.5 Km/s.
The data was a band-limited impulse (5-40 Hz)
delayed .5 seconds and placed
at .5 Km offset along the azimuthal direction.
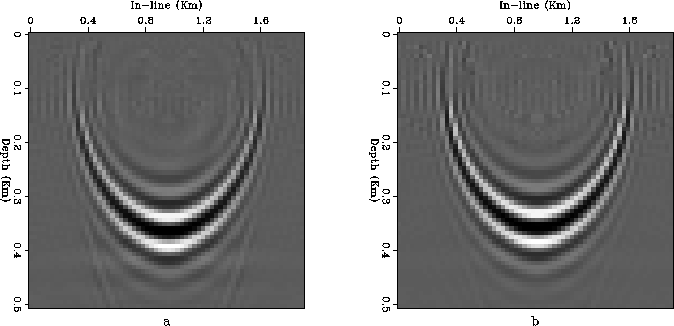
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a vertical slice along the
azimuthal direction of the migration results for both
the 5-D phase-shift migration (a) and the common-azimuth
phase-shift migration (b).
Figure
shows a vertical slice along the
azimuthal direction of the migration results for both
the 5-D phase-shift migration (a) and the common-azimuth
phase-shift migration (b).
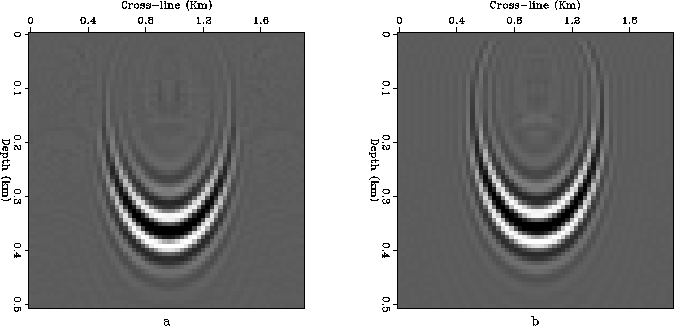
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the horizontal slices taken
across the migration results
at constant depth of 160 m.
There are very small differences between the results;
they are mostly caused by numerical artifacts that are larger
in the 5-D phase-shift results.
We somewhat undersampled the cross-azimuth offset axis
of the full 5-D dataset,
to accommodate limitations of our test program
in handling out-of-core jobs.
shows the horizontal slices taken
across the migration results
at constant depth of 160 m.
There are very small differences between the results;
they are mostly caused by numerical artifacts that are larger
in the 5-D phase-shift results.
We somewhat undersampled the cross-azimuth offset axis
of the full 5-D dataset,
to accommodate limitations of our test program
in handling out-of-core jobs.
 |
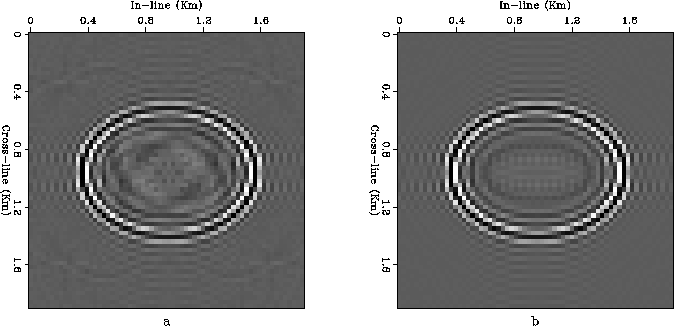 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare the results obtained by applying common-azimuth
Stolt migration (b) and 5-D phase shift migration (a).
The differences between the results are mainly
in the numerical artifacts, though the amplitudes
behavior is also slightly different.
This inaccuracy in amplitudes is probably
caused by the neglect of the amplitude term
compare the results obtained by applying common-azimuth
Stolt migration (b) and 5-D phase shift migration (a).
The differences between the results are mainly
in the numerical artifacts, though the amplitudes
behavior is also slightly different.
This inaccuracy in amplitudes is probably
caused by the neglect of the amplitude term ![]() in equation Stolt_mig.eq, as we discussed in the previous section.
in equation Stolt_mig.eq, as we discussed in the previous section.
 |
 |
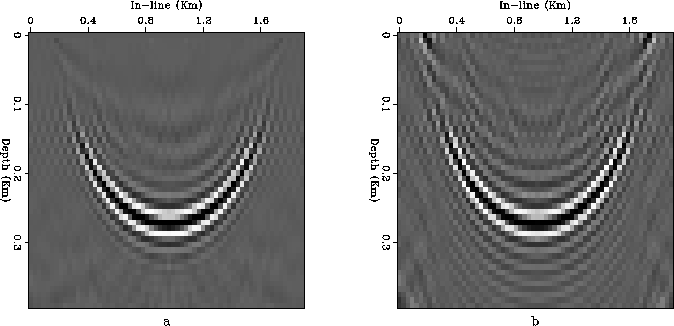
To test the accuracy of phase-shift common-azimuth migration
for varying velocity
we migrated the same dataset as in the constant velocity test,
but with velocity increasing with depth.
The velocity function had a constant but strong (5 s-1)
vertical gradient.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the vertical sections along the
azimuthal direction of the migrated results
obtained by the full 5-D phase-shift method (a)
and the 4-D common-azimuth one (b).
Figure
compares the vertical sections along the
azimuthal direction of the migrated results
obtained by the full 5-D phase-shift method (a)
and the 4-D common-azimuth one (b).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the vertical sections along
the cross-azimuth direction.
Because of the strong vertical gradient the impulse responses
are not semicircle, but they bulge outwardly in the shallow
part of the section.
Finally Figure
compares the vertical sections along
the cross-azimuth direction.
Because of the strong vertical gradient the impulse responses
are not semicircle, but they bulge outwardly in the shallow
part of the section.
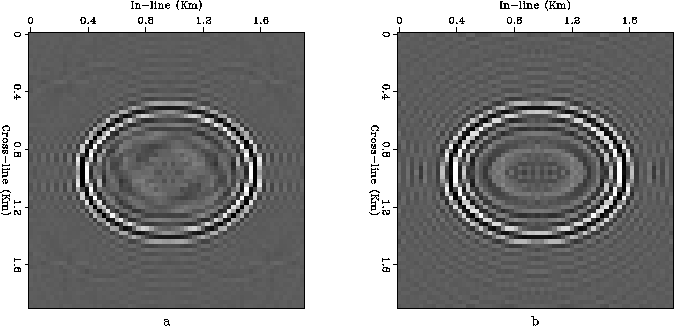
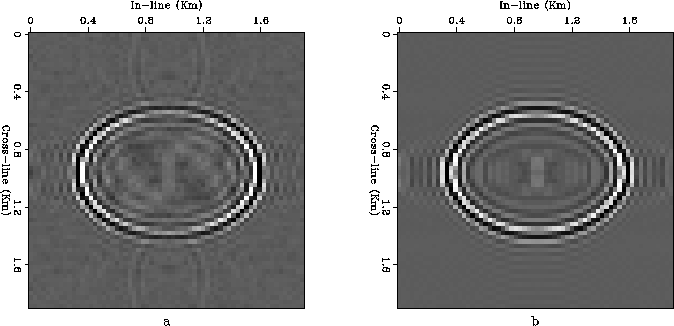
Finally Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the horizontal sections
taken from the migrated results at a depth of 160 m.
There are slight differences between the migration results obtained
using the two phase-shift methods.
The most noticeable are in the amplitudes behavior as a
function of the reflector dips
(Figures
compares the horizontal sections
taken from the migrated results at a depth of 160 m.
There are slight differences between the migration results obtained
using the two phase-shift methods.
The most noticeable are in the amplitudes behavior as a
function of the reflector dips
(Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The common-azimuth migration shows higher amplitudes for the
steeply dipping reflectors.
There are also slight differences in the phases
of the results.
These phase errors
are only visible in the depth slices
because they vanish along the axis
and they are maximum along the direction oriented
at an angle of 45 degrees with respect to the axis.
However, overall
the common-azimuth migration produced a fairly accurate result,
notwithstanding the strong velocity gradient.
).
The common-azimuth migration shows higher amplitudes for the
steeply dipping reflectors.
There are also slight differences in the phases
of the results.
These phase errors
are only visible in the depth slices
because they vanish along the axis
and they are maximum along the direction oriented
at an angle of 45 degrees with respect to the axis.
However, overall
the common-azimuth migration produced a fairly accurate result,
notwithstanding the strong velocity gradient.
 |
 |
 |
CONCLUSIONS 3-D common-azimuth datasets can be efficiently migrated in the frequency-wavenumber domain with methods based on the one-way wave equation (Stolt and phase-shift) thanks to a stationary-phase approximation that reduces the dimensionality of the computational space from five to the original four of the common-azimuth geometry. Within the stationary phase assumptions, the proposed methods are exact for constant velocity. For velocity functions varying with depth we have introduced an approximation that leads to an efficient recursive (phase-shift) algorithm. When our approximation is used for migrating synthetic data in presence of strong vertical gradient in velocity the results are very close to the result obtained using a full 5-D phase-shift method.
We would like to thank Dave Nichols and François Audebert for many insightful discussions.
[SEP,com_azim]
A
DERIVATION OF COMMON-AZIMUTH PHASE-SHIFT MIGRATION
In this appendix we derive the stationary-phase approximation
for common-azimuth phase-shift migration.
We start by analyzing the adjoint operation;
that is, the forward modeling of common-azimuth data.
This side-step is not necessary for the derivation of phase-shift
common-azimuth migration, but it makes the phase-shift case
parallel to the development of Stolt common-azimuth migration
(Appendix B) and thus we think that both
derivations become clearer.
The prestack data in the wavenumber domain
can be obtained
by summing the contributions of the reflectors
at each depth level appropriately delayed (phase shifted in the
wavenumber domain) according to the double-square root equation.
In mathematical terms the prestack data in
the temporal frequency (![]() ),
the midpoint wavenumbers
),
the midpoint wavenumbers ![]() ),
and the offset wavenumbers
),
and the offset wavenumbers ![]() )are given by the following integral
)are given by the following integral
| (9) |
| (10) |
![\begin{eqnarray}
\lefteqn{DSQR(\omega,{\bf k}_{m},{\bf k}_{h},z^{'})=} \nonumber...
...(k_{mx}-k_{hx}\right)^2 + \left(k_{my}-k_{hy}\right)^2 ]} \right\}\end{eqnarray}](img9.gif) |
||
| (11) |
The common-azimuth data corresponding to the azimuth oriented along the in-line direction x can be extracted from the full prestack dataset by integrating the data over all the khy wavenumbers. The expression for computing a common azimuth dataset is
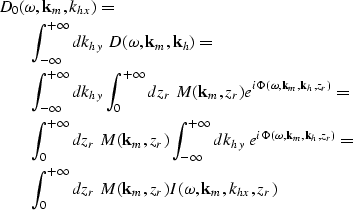 |
||
| (12) |
In the stationary-phase regime, the second integral ![]() can be asymptotically approximated by
can be asymptotically approximated by
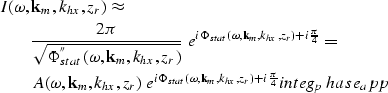 |
||
| (13) |
Constant velocity
For constant velocity the integral in the expression for the phase function is easily evaluated and the phase function simplifies to
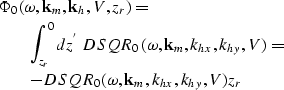 |
||
| (14) |
Consequently, in constant velocity the stationary path for the phase function is equal to the stationary path for the double-square root equation and it can be evaluated analytically. There are two solutions for the stationary path of the double-square root equation, and they are
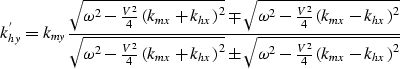 |
(15) |
Velocity function of depth
When velocity varies with depth the integral in the expression for the phase function [equation phase_funct_ph.eq] cannot be evaluated analytically. Consequently the ``global'' stationary path cannot be derived analytically, and its numerical computation is expensive. However, from the constant velocity case, we can analytically derive the ``local'' stationary paths at each depth level,
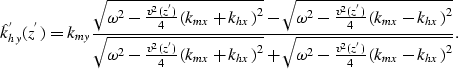 |
(16) |
| (17) |
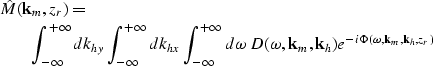 |
||
| (18) |
| (19) |
As for modeling, this expression for migration is exact (within the approximation of stationary phase) for constant velocity, but it is approximated for velocity varying with depth.
B
DERIVATION OF COMMON-AZIMUTH STOLT MIGRATION
In this appendix we derive the stationary-phase approximation
for Stolt common-azimuth migration. As for the phase-shift case,
we start from the stationary-phase approximation of Stolt modeling.
The 3-D prestack data in time (t),
the midpoint wavenumber ![]() ),
and the offset wavenumber
),
and the offset wavenumber ![]() )can be computed by Stolt modeling using
the following integral over the pseudo-depth
)can be computed by Stolt modeling using
the following integral over the pseudo-depth ![]() ,
,
| (20) |
| (21) |
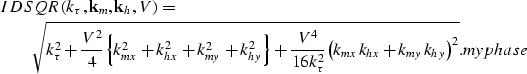 |
||
| (22) |
The common-azimuth data corresponding to the azimuth oriented along the in-line direction x can be extracted from the full prestack dataset by integrating the data over all the khy wavenumbers. The expression for computing a common azimuth dataset is
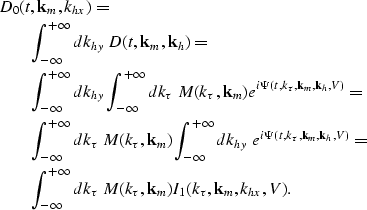 |
||
| (23) |
In the stationary-phase regime, the second integral ![]() can be asymptotically approximated by
can be asymptotically approximated by
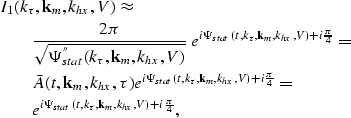 |
||
| (24) |
| (25) |
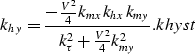 |
(26) |
| (27) |
| (28) |
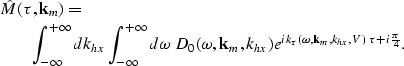 |
||
| (29) |
| (30) |
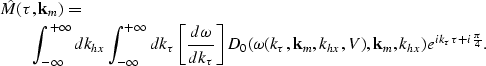 |
||
| (31) |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)