




Next: OFFSET SEPARATION
Up: Introduction
Previous: Introduction
Constant velocity prestack migration
in offset-midpoint coordinates (Yilmaz, 1979) can be formulated as:
| 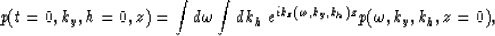 |
(1) |
where 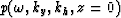 is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
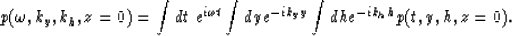
The phase 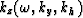 is defined in the
dispersion relation as
is defined in the
dispersion relation as
| ![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left\{ \...
...r v^2} -
{1 \over 4}(k_y-k_h)^2\right]^{1 \over 2} \right\} },\end{displaymath}](img5.gif) |
(2) |
which is also referred to as the double square-root (DSR) equation.
The two integrals in  and kh in equation (1)
represent the imaging
condition for zero-offset and zero time (h=0,t=0).
and kh in equation (1)
represent the imaging
condition for zero-offset and zero time (h=0,t=0).
In equation (1), the values of kz
have to be real. Imaginary values of kz do not
satisfy the downward continuation ordinary differential
equation
| 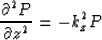 |
(3) |
and have to be excluded. Real values of kz
in equation (2) require both of the following
conditions to be satisfied:
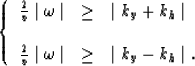
By considering the four possible sign cases, given by assigning
ky and kh
positive and negative values, these two conditions can be reduced
to the condition:
| 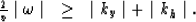 |
(4) |
Equation (4) will prove to be crucial in
determining the source of artifacts that appear in constant-offset
migrated sections (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a).
a).
The prestack DSR algorithm using constant sampling in kh
can be summarized as:
FFT along all axes 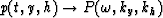 do z
do ky
do
do z
do ky
do  do kh
if
do kh
if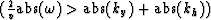 then
then
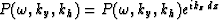
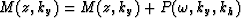 endif
endif
Note that in order to perform an FFT along the offset axis, the variable
kh is evenly sampled between the
Nyquist negative and positive values.
However, due to
condition (4), for each set of 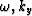 the
loop in kh will use either a subset or all of the possible
kh sampled values.
the
loop in kh will use either a subset or all of the possible
kh sampled values.





Next: OFFSET SEPARATION
Up: Introduction
Previous: Introduction
Stanford Exploration Project
11/16/1997
![]()
![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\rm sign}(\omega) \left\{ \...
...r v^2} -
{1 \over 4}(k_y-k_h)^2\right]^{1 \over 2} \right\} },\end{displaymath}](img5.gif)
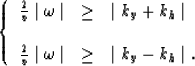
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a).
a).
do z do ky do
do kh if
then
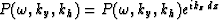
endif
![]() the
loop in kh will use either a subset or all of the possible
kh sampled values.
the
loop in kh will use either a subset or all of the possible
kh sampled values.