VALUE OF DATA EXTENSION

The value of extending the data should not be judged on results shown above. First, the extension methodology is new and there was no time to tune the parameters. Another unfamiliar new problem is that logarithms have an additive constant that I was unsure of how to optimize. My motivation for the extension was caused by observing steady growth of side boundary effects (midpoint axis) as the number of iterations in the tomography problem increased. Keep in mind the background that this data set is 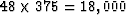$48\times 375=18,000$ points so assuming we seek a model space of the same number of points, the solver theoretically requires 18,000 iterations. My experimental work was limited to 5-25 iterations. A question in my mind was and is, how close are these solutions to the final limit? I hypothesize that truncation of a data set could severely limit the rate of convergence during the first 5-25 iterations and that extending the data would accelerate convergence. Time did not allow adequate testing of this interesting hypothesis.

I also saw that the solution deteriorates in an interesting manner at high iterations. Damping can be installed in the tomography, but I had no time to experiment or think of the theory. I wondered how the above problems would be affected by extending the data, which seemed to help, but which seems to have been less important than other variables, particularly, the iteration count.

An overarching doubt is whether the underlying absorption model warrants any more effort, since I believe that focusing is a more likely model.