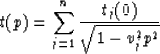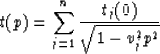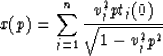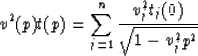A bunch of isotropic layers

From these and previous results it follows that we have these relationships for travel-time, offset, and velocity of a stack of n layers as a function of p.

$$t(p) = \sum_{j=1}^{n}\frac{t_{j}(0)}{\sqrt{1-v_{j}^{2}p^{2}}}$$

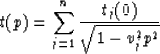
and

$$x(p) = \sum_{j=1}^{n}\frac{v_{j}^{2}pt_{j}(0)}{\sqrt{1-v_{j}^{2}p^{2}}}$$

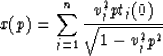
and

$$v^{2}(p)t(p) = \sum_{j=1}^{n}\frac{v_{j}^{2}t_{j}(0)}{\sqrt{1-v_{j}^{2}p^{2}}}$$

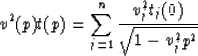
This last relation is particularly useful, since it gives us the means for distinguishing whether non-hyperbolic move-out is due to anisotropy or heterogeneity. A simple scheme might look like this:

1.

determine v(p) for each reflector.

2.

Decompose these velocity functions into their interval counterparts.

3.

Test each interval v(p) for closeness to isotropy.

Simply put, those layers whose interval velocities are p-independent are isotropic (or maybe elliptic).