Next: Using the Eikonal equation
Up: USING 3-D EIKONAL EQUATION
Previous: USING 3-D EIKONAL EQUATION
In the 3-D case, the wave equation corresponding to the ray-theoretic
interpretation of all-angle time migration is
| 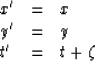 |
(11) |
in the 3-D time-retarded coordinate system
| 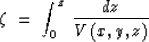 |
(12) |
with the new time-like vertical coordinate 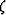 ,
,
| 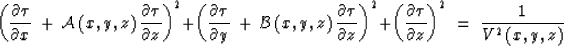 |
(13) |
Following the same scheme as for the 2-D case and using equations
(12) and (13), we finally obtain the 3-D Eikonal
equation for time migration:
| 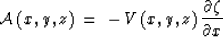 |
(14) |
with
| 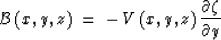 |
(15) |
and





Next: Using the Eikonal equation
Up: USING 3-D EIKONAL EQUATION
Previous: USING 3-D EIKONAL EQUATION
Stanford Exploration Project
11/17/1997