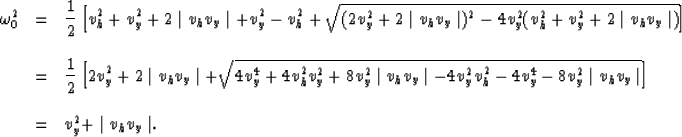Next: About this document ...
Up: Popovici : DMO &
Previous: CONCLUSIONS
- Biondi, B., and Ronen, J., 1987,
Dip moveout in shot profiles:
Geophysics, 52, 1473-1482.
- Black, J.L., Schleicher, K.L., and Zhang, L., 1993,
True-amplitude imaging and dip moveout:
Geophysics, 58, 47-66.
- Deregowski, S. M., and Rocca, F., 1981,
Geometrical optics and wave theory of constant-offset sections
in layered media: Geophysical Prospecting, 29, 374-406.
- Jakubowitz, H., 1990, A simple efficient method of dip-moveout
correction: Geophysical Prospecting, 38, 221-245.
- Hale, I. D., 1983, Dip-moveout by Fourier
transform: Ph.D. thesis, Stanford University.
- Popovici, A.M., 1993,
Partial Differential Equation for Migration to Zero-Offset:
SEP-77, 77-88.
- Yilmaz, O., and Claerbout, J. F., 1980,
Prestack partial migration:
Geophysics, 45, 1753-1779.
- Zhang, L., 1988,
A new Jacobian for dip moveout: SEP-59, 201-208.
APPENDIX A
The purpose of this appendix is to express
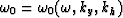 and to
find the integration limits for
and to
find the integration limits for 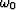 given
the integration limits for
given
the integration limits for 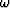 . Start
with the expression for
. Start
with the expression for 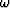 :
:
| 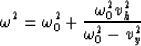 |
(20) |
and after reducing
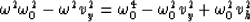
and grouping
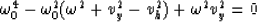
we have
| 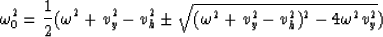 |
(21) |
The discriminant 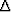 is
is
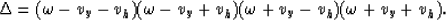
From the conditions on kz in equation (12),
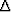 is always positive
and therefore
is always positive
and therefore 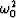 is real.
is real.
The integration limits for 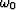 are found by
starting with the limits
are found by
starting with the limits 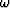 :
:
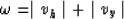
and after we square both sides
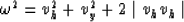
and replacing 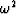 in the equation for
in the equation for 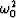 we have
we have
| 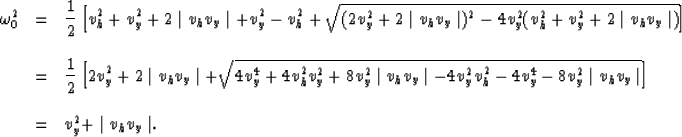 |
(22) |





Next: About this document ...
Up: Popovici : DMO &
Previous: CONCLUSIONS
Stanford Exploration Project
11/17/1997
![]() and to
find the integration limits for
and to
find the integration limits for ![]() given
the integration limits for
given
the integration limits for ![]() . Start
with the expression for
. Start
with the expression for ![]() :
:
![]()
![]()
![]()
![]() are found by
starting with the limits
are found by
starting with the limits ![]() :
:
![]()
![]()