By taking equation (14)
and changing the integration
variable from ![]() to
to ![]() . In the
same time the new variable
. In the
same time the new variable ![]() becomes function of only two variables in
becomes function of only two variables in ![]() ,in the form given by equation (11).
,in the form given by equation (11).
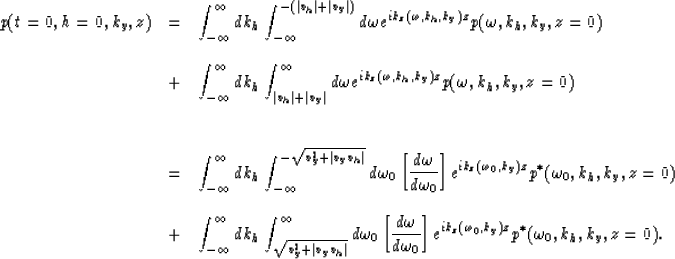 |
(16) |
Special attention should be given to the new field
![]() . As the variable
. As the variable
![]() is replaced with
is replaced with ![]() , each value of
, each value of ![]() has to be associated with the appropriate value of the field
has to be associated with the appropriate value of the field
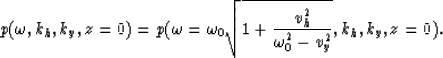
From equation (10) the Jacobian is
| |
(17) |
In the next step we change the integration order
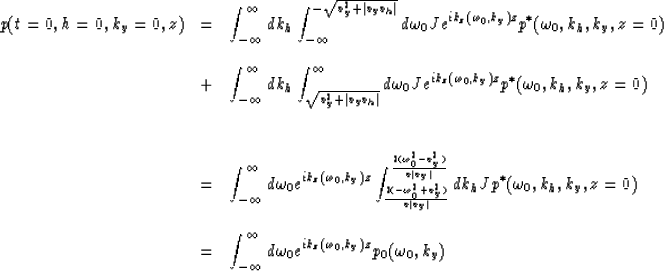 |
(18) |
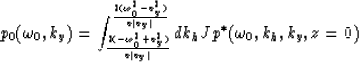 |
(19) |
Equation (18) represents zero-offset downward continuation and imaging as introduced by Gazdag (1978) or Stolt (1978). Equation (19) represents a way of obtaining zero-offset section from constant-offset sections.
The operations needed to obtain the zero-offset stacked section from the constant-offset field described in equation (19) are: