Next: About this document ...
Up: Popovici : PDE for
Previous: Acknowledgments
- Claerbout, J. C., 1985, Imaging the Earth's Interior:
Blackwell Scientific Publications.
- Deregowski, S. M., and Rocca, F., 1981,
Geometrical optics and wave theory of constant-offset sections
in layered media: Geophysical Prospecting, 29, 374-406.
- Gazdag, J., 1978,
Wave equation migration with the phase shift method:
Geophysics, 43, 1342-1351.
- Hale, I. D., 1983, Dip-moveout by Fourier
transform: Ph.D. thesis, Stanford University.
- Hale, I. D., 1988, Dip-moveout processing:
Course notes from SEG continuing education course, SEG.
- Popovici, A. M., 1990,
Prestack partial migration analysis:
SEP-65, 17-28.
- Popovici, A. M., 1992, Dip-Moveout processing:
A Tutorial. DMO basics and DMO by Fourier transform:
SEP-75, 407-425.
- Stolt, R.H., 1978,
Migration by Fourier transform:
Geophysics, 43, 23-48.
- Zhang, L., 1988,
A new Jacobian for dip moveout: SEP-59, 201-208.
APPENDIX A
In equation (1) the values of the constant kz,
given by equation (2),
have to be real. Imaginary values of kz do not
satisfy the downward continuation ordinary differential
equation
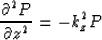
and have to be excluded. Real values of kz
from equation (2) require the conditions:
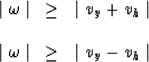
which can be reduced to the condition
| 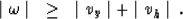 |
(16) |
After the change of variable from 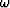 to
to 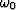 in equation (5)
in equation (5)
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img15.gif)
we want to express 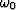 function of
function of 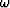 and
determine the integration boundaries for
and
determine the integration boundaries for 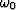 .We start
with the expression for
.We start
with the expression for 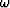 :
:
| 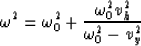 |
(17) |
and after reducing
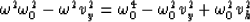
and grouping
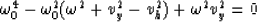
we have
| 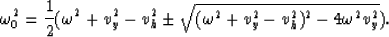 |
(18) |
The discriminant 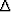 is
is
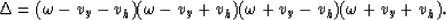
From the conditions on kz, 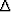 is always positive
and therefore
is always positive
and therefore 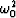 is always real within
the
is always real within
the 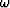 limits.
limits.
The integration limits for 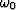 are found by
starting with the limits for
are found by
starting with the limits for 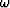 :
:
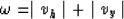
and after we square both sides
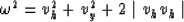
and replacing 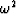 in the equation for
in the equation for 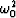 we have
we have
| 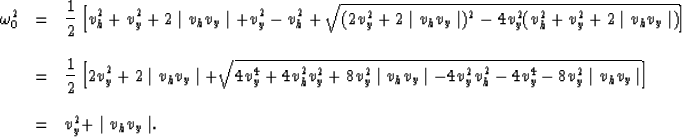 |
(19) |
The integration in 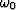 is done from
is done from
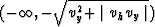 and from
and from
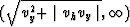 . After changing
the order of integration from
. After changing
the order of integration from 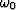 to kh, the
integration boundaries for kh become
to kh, the
integration boundaries for kh become
| 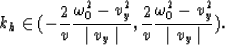 |
(20) |





Next: About this document ...
Up: Popovici : PDE for
Previous: Acknowledgments
Stanford Exploration Project
11/17/1997
![]()
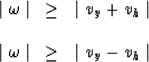
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img15.gif)
![]()
![]()
![]()
![]() are found by
starting with the limits for
are found by
starting with the limits for ![]() :
:
![]()
![]()