| (3) |
| (4) |
| (5) |
| |
(6) |
where
v : velocity field
![]() : traction field
: traction field
v+ : upgoing wave amplitude
v- : downgoing wave amplitude
z : layer thickness
![]() : density of each layer
: density of each layer
s : compliance of the layer
Let ![]() a building block matrix in i-th layer. Then,
a building block matrix in i-th layer. Then,
| |
(7) |
| (8) |
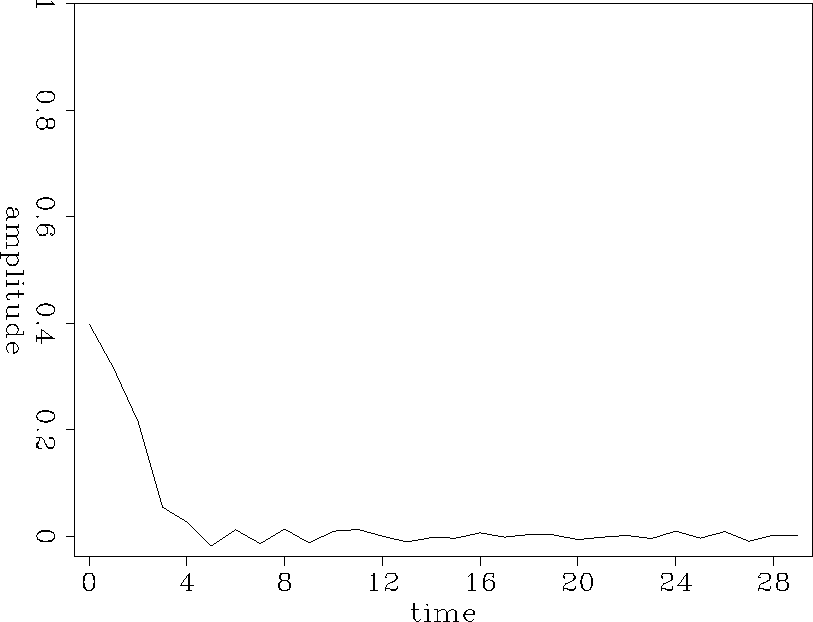
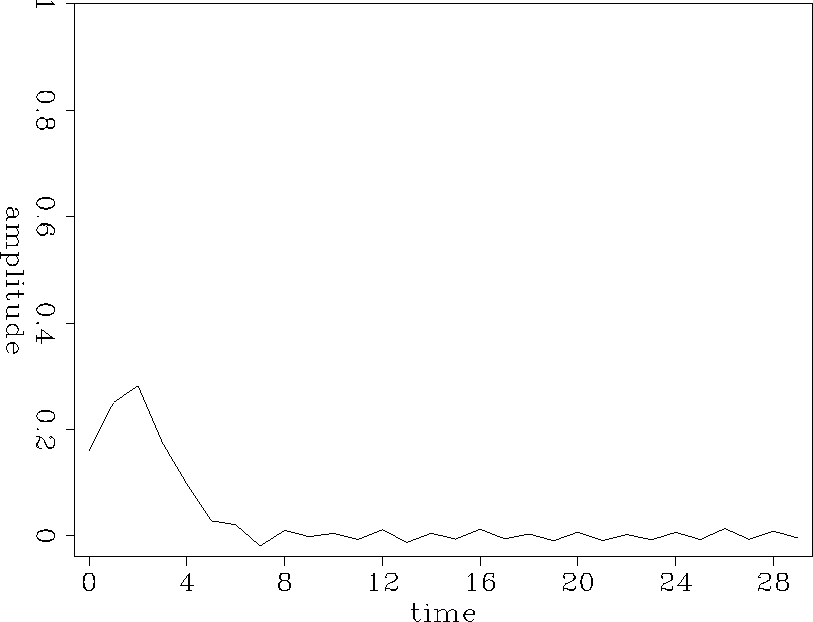
An impulse of amplitude 1 is used as an input. The output is averaged over 32 different random sequences with the same statistical properties. The experiment is done for various numbers of layers to see how the number of layers affects the output. The numbers used here are powers of 2, say 32,64,128. To make problem simpler, the velocities of the two states are chosen to be the same. The time sampling interval is equal to the difference between the arrival time of the primary and that of the shortest path multiple. The frame is retarded by the amount of the first arrival time. Figure 1-4 show the impulse responses for the different four numbers of layers.
 |
 |
 |
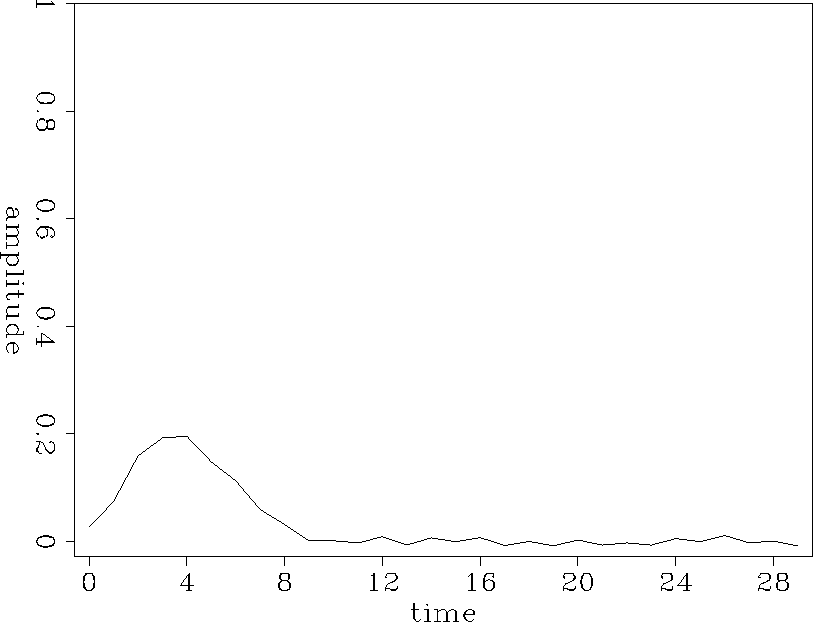 |
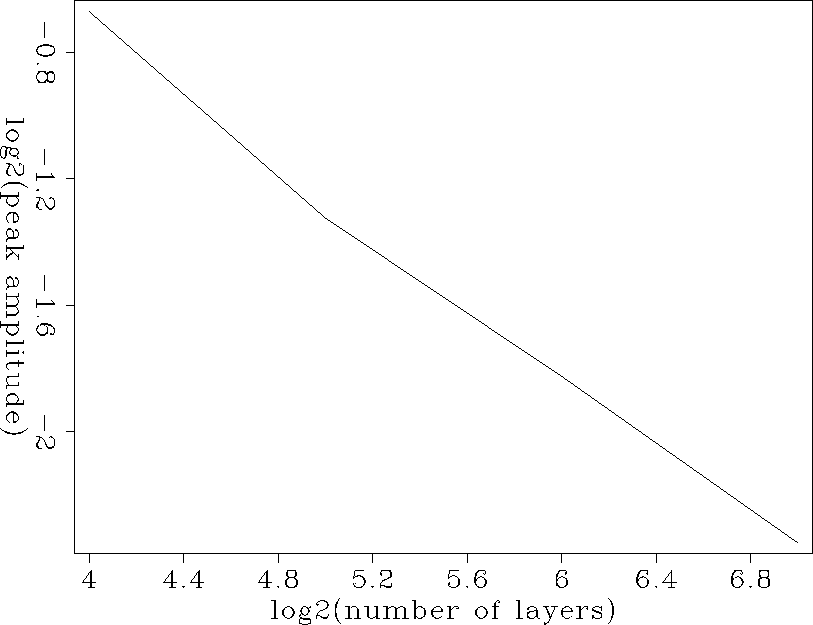
As expected, the impulse broadens as the number of layers increases. The peak arrival time is retarded accordingly. The peak amplitude decays approximately in proportion to the square root of the number of layers. Figure 5 shows this relationship. The retarded time of the peak amplitude from the primary is proportional to the number of the layers.
 |