




Next: THE SCHOENBERG-MUIR CALCULUS
Up: Dellinger & Muir: Dix
Previous: The spring group
The method we have used to solve the simple spring problem is quite general
and applies equally well to other layered-medium problems, for
example the calculus of Schoenberg-Muir and the Dix equations.
For this reason it is worthwhile to pause here and enumerate
the steps we used explicitly:
- [1)] Find the general equation describing layer behavior
(e.g., equation (5)).
- [2)] Divide the variables that occur in the general layer equation
into three classes:
- [2a)] The layer parameters are assumed given (e.g., the ki).
- [2b)] The constant parameters have the same value for all layers
in the stack (e.g., F).
- [2c)] The additive parameters sum through the stack
(e.g., the
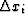 ).
).
- [3)] Rewrite the equation from step 1 so it has the form
| 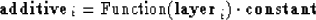 |
(12) |
(e.g., equation (8)).
- [4)] Identify the term ``
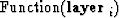 ''
as an alternative layer-group representation of the layer parameters
(e.g., the 1/ki). To find the homogeneous equivalent of a stack, convert
from the standard representation to the layer group, sum, and convert back.
''
as an alternative layer-group representation of the layer parameters
(e.g., the 1/ki). To find the homogeneous equivalent of a stack, convert
from the standard representation to the layer group, sum, and convert back.





Next: THE SCHOENBERG-MUIR CALCULUS
Up: Dellinger & Muir: Dix
Previous: The spring group
Stanford Exploration Project
11/17/1997
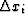 ).
).