| |
(1) |
For a wave field transformation from one datum to another, the discretized form of equation (1) is a summation where each input trace Ui is weighted and time shifted. Each output trace is calculated by performing a sum of the form:
| |
(2) |
Figure 1 illustrates the impulse response of upward continuation
and downward continuation for three diffractors at three different depths.
The energy from each diffractor is distributed along a hyperbolic trajectory.
The trajectory is the same for all depths.
It is natural and convenient to do the calculation in the frequency domain
because each input trace is shifted by a time invariant amount.
The algorithm is cast in ![]() domain
so that each individual output trace is calculated by
performing a sum of the form:
domain
so that each individual output trace is calculated by
performing a sum of the form:
| |
(3) |
|
updnimp1
Figure 1 Impulse response of three diffractors at three different depths for upward continuation and downward continuation. If you have the electronic version of this document, you can press the button to see a movie of the impulse response for diffractors at different depths. | 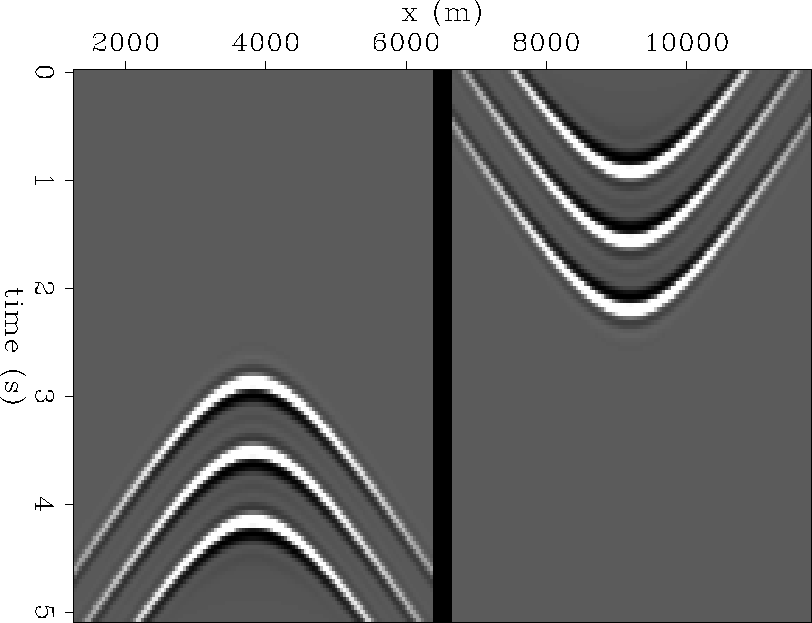 |
Kirchhoff datuming is typically implemented in a serial fashion by looping over the input traces as indicated by equations (2) and (3). The algorithm can be applied to zero-offset data or to shot and receiver gathers. Pre-stack datuming is done by extrapolating the shots and the geophones separately using equation (3) Berryhill (1984). The extension to three dimensions is straight forward and has the same algorithmic form. Equations (1) through (3) are for upward continuation. For downward continuation the conjugate transpose process is used.