




Next: Reflection angle estimation
Up: THEORY
Previous: Inverse problem
Under the stationary phase approximation, the 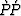 equation is in the
standard linear form:
equation is in the
standard linear form: 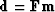 . This has a well-known damped least-squares
Gauss-Newton solution:
. This has a well-known damped least-squares
Gauss-Newton solution:
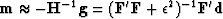 , where
, where
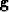 and
and 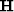 are the gradient and Hessian of E respectively, and
are the gradient and Hessian of E respectively, and
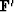 is the adjoint operator. In this case, the gradient can be derived as
is the adjoint operator. In this case, the gradient can be derived as
| 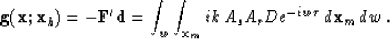 |
(4) |
where 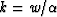 is the spatial wavenumber.
An approximate diagonal Hessian can be derived as
is the spatial wavenumber.
An approximate diagonal Hessian can be derived as
| 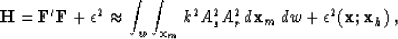 |
(5) |
resulting in the l2 reflectivity solution
| 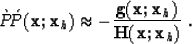 |
(6) |
The approximate
diagonal Hessian solution (6) costs little more to implement
than a standard prestack migration, but requires twice the memory
in order to store the gradient and Hessian images separately.
In particular, (6) involves two separate but simultaneous images
to be evaluated, the gradient (numerator) being a weighted Kirchhoff
prestack depth migration, and the approximate Hessian (denominator)
being an accumulation of the squared migration weights.





Next: Reflection angle estimation
Up: THEORY
Previous: Inverse problem
Stanford Exploration Project
11/17/1997
![]() equation is in the
standard linear form:
equation is in the
standard linear form: ![]() . This has a well-known damped least-squares
Gauss-Newton solution:
. This has a well-known damped least-squares
Gauss-Newton solution:
![]() , where
, where
![]() and
and ![]() are the gradient and Hessian of E respectively, and
are the gradient and Hessian of E respectively, and
![]() is the adjoint operator. In this case, the gradient can be derived as
is the adjoint operator. In this case, the gradient can be derived as