RECTANGULAR COORDINATES

In a 2-D rectangular coordinate frame the wave equation in the time domain is given by,

$$\frac{\partial^2 P }{ \partial z^2 } + \frac{\partial^2 P}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 P }{ \partial t^2 }$$

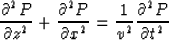
When this equation is Fourier transformed over time and x we obtain,

$$\frac{\partial^2 P }{ \partial z^2 } -k_x^2 P = -\frac{\omega^2}{v^2} P$$

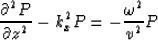
or,

$$\frac{\partial^2 P }{ \partial z^2 } = \left[ k_x^2 -\frac{\omega^2}{v^2} \right] P$$

If we assume a solution of the form,

P(z) = P(z₀) e ^{i k_z ( z- z₀ )} ,

we find  

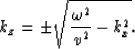$$k_z = \pm \sqrt {\frac{\omega^2}{v^2} - k_x^2}.$$ (1)

Given a solution at one depth level P(z) we can extrapolate it to a new depth level using a pure phase shift 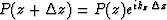$P( z+ \Delta z) = P(z) e^{ i k_z \Delta z}$.The positive square root is chosen for positive frequencies in order to select waves that propagate downwards as time increases.

Using this method we can propagate an initial condition specified at z=0 to any depth by applying suitable phase shifts at each depth level.