




Next: Conclusions
Up: Nichols: Modeling in polar
Previous: More complicated coordinate frames
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the modeling results for a v(z) medium
with a strong velocity gradient (10 ms-1/m). In this medium the
wavefronts overturn. The rectangular coordinate modeling code does
not model these waves because the wavefield is always extrapolated
downwards and any energy in the evanescent zone (with a dip greater
than
shows the modeling results for a v(z) medium
with a strong velocity gradient (10 ms-1/m). In this medium the
wavefronts overturn. The rectangular coordinate modeling code does
not model these waves because the wavefield is always extrapolated
downwards and any energy in the evanescent zone (with a dip greater
than 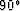 ) is removed at each downwards extrapolation step.
However it is surprising to see energy in the rectangular coordinate
frame that is apparently upgoing. This is a byproduct of the high velocity
gradient, the energy has a phase slowness that points horizontally but
a group slowness that points upwards. There is less energy in the
``overturned'' region that there should be, because the true overturned
energy has not been modeled. The two polar coordinate frames show the
correct amount of overturned energy. In this particular example the
) is removed at each downwards extrapolation step.
However it is surprising to see energy in the rectangular coordinate
frame that is apparently upgoing. This is a byproduct of the high velocity
gradient, the energy has a phase slowness that points horizontally but
a group slowness that points upwards. There is less energy in the
``overturned'' region that there should be, because the true overturned
energy has not been modeled. The two polar coordinate frames show the
correct amount of overturned energy. In this particular example the
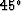 result may be better that the PSPI result in polar
coordinates. This is because the very strong gradient is not well
handled by the PSPI algorithm. The gradient affects the polar
coordinate PSPI code because there is a strong gradient in
result may be better that the PSPI result in polar
coordinates. This is because the very strong gradient is not well
handled by the PSPI algorithm. The gradient affects the polar
coordinate PSPI code because there is a strong gradient in 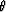 ,even though there in no gradient in x.
,even though there in no gradient in x.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows another result with upgoing energy. In
this case the energy may not be desirable. The model is a two layer
medium with a step function in velocity at 300m. The rectangular
coordinate frame phase shift result shows only downgoing waves. In
contrast the two polar coordinate results display a small piece of
reflected energy. This is energy that is upgoing, but still outgoing!
Once the angle of incidence exceeds
shows another result with upgoing energy. In
this case the energy may not be desirable. The model is a two layer
medium with a step function in velocity at 300m. The rectangular
coordinate frame phase shift result shows only downgoing waves. In
contrast the two polar coordinate results display a small piece of
reflected energy. This is energy that is upgoing, but still outgoing!
Once the angle of incidence exceeds 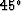 to the vertical the
reflected energy is propagated outwards in the polar coordinate frame.
There is also some dispersed energy in the
to the vertical the
reflected energy is propagated outwards in the polar coordinate frame.
There is also some dispersed energy in the 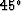 result. This is
probably due to reflected energy that travels at more than
result. This is
probably due to reflected energy that travels at more than 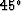 to the polar grid and is thus poorly modeled.
to the polar grid and is thus poorly modeled.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of modeling in a medium with
a small low velocity anomaly. The anomaly is a Gaussian blob with
a half width of 100m. Apart from the loss of high dips in the rectangular
coordinate frame, all three methods produce similar results. The main
difference is that the
shows the result of modeling in a medium with
a small low velocity anomaly. The anomaly is a Gaussian blob with
a half width of 100m. Apart from the loss of high dips in the rectangular
coordinate frame, all three methods produce similar results. The main
difference is that the 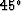
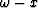 method was much cheaper
to produce.
method was much cheaper
to produce.





Next: Conclusions
Up: Nichols: Modeling in polar
Previous: More complicated coordinate frames
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the modeling results for a v(z) medium
with a strong velocity gradient (10 ms-1/m). In this medium the
wavefronts overturn. The rectangular coordinate modeling code does
not model these waves because the wavefield is always extrapolated
downwards and any energy in the evanescent zone (with a dip greater
than
shows the modeling results for a v(z) medium
with a strong velocity gradient (10 ms-1/m). In this medium the
wavefronts overturn. The rectangular coordinate modeling code does
not model these waves because the wavefield is always extrapolated
downwards and any energy in the evanescent zone (with a dip greater
than