Next: DISCUSSION
Up: INTERPOLATION STRATEGIES
Previous: Nearest neighbor in time,
In the case of bilinear interpolation, the approximate function is given by,
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the geometry associated with bilinear
interpolation within a cell.
illustrates the geometry associated with bilinear
interpolation within a cell.
bilin
Figure 10 Bilinear
interpolation. The function is approximated by bilinear interpolation within a
cell defined by the four corner samples. The interpolation weights depend on
the coordinates at which the path enters an leaves the cell.

The path within the cell, t(x), is approximated by a linear segment,
![\begin{displaymath}
\hat{t}(x) = t(\xi_0) \left[1 - \frac{x - \xi_0}{\xi_1-\xi_0}\right] +
t(\xi_1)\left[ \frac{x - \xi_0}{\xi_1-\xi_0} \right] \end{displaymath}](img17.gif)
The Mathematica code in the appendix will calculate the appropriate
weights for each sample point. For example, the weight to be applied
to the sample point (xix,tit) is:
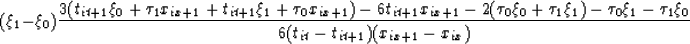
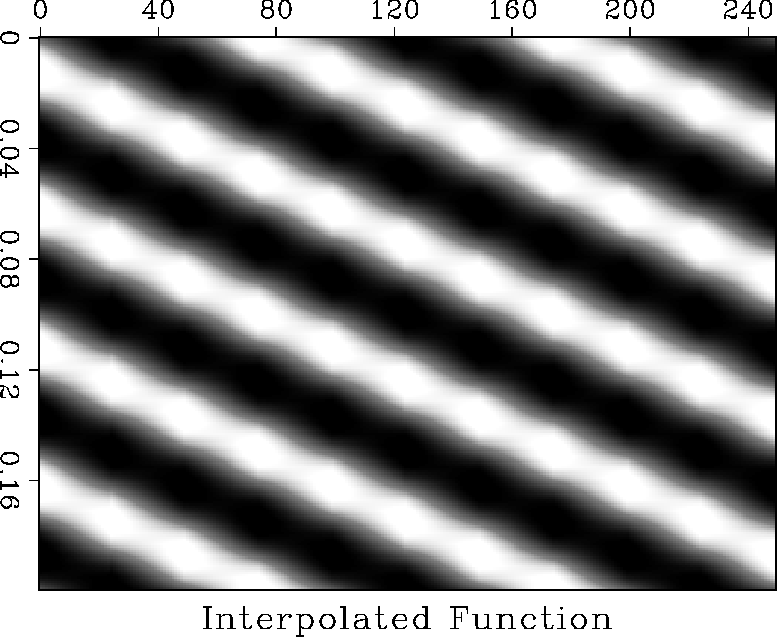
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the approximation to the original
function surface that is implied by this method. For this set of
parameters it is a reasonable approximation of the original surface.
In general bilinear interpolation is a reasonable interpolation method
for sampling intervals up to about half of the Nyquist frequency. If the
data has high dips and high frequencies the approximation may not be
valid.
shows the approximation to the original
function surface that is implied by this method. For this set of
parameters it is a reasonable approximation of the original surface.
In general bilinear interpolation is a reasonable interpolation method
for sampling intervals up to about half of the Nyquist frequency. If the
data has high dips and high frequencies the approximation may not be
valid.
bilin-func
Figure 11 Input data sampled every 4ms in time
and 25m in space and then interpolated using bilinear interpolation in
space and time.










Next: DISCUSSION
Up: INTERPOLATION STRATEGIES
Previous: Nearest neighbor in time,
Stanford Exploration Project
11/17/1997
![\begin{eqnarraystar}
\hat{f}( x, t ) & = &
\tilde{f}( ix-1, it-1 )\left[1 - \fra...
...\right]
\left[\frac{ t - t_{it-1} }{t_{it} - t{it-1} }\right]\end{eqnarraystar}](img16.gif)
![\begin{eqnarraystar}
\hat{f}( x, t ) & = &
\tilde{f}( ix-1, it-1 )\left[1 - \fra...
...\right]
\left[\frac{ t - t_{it-1} }{t_{it} - t{it-1} }\right]\end{eqnarraystar}](img16.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the geometry associated with bilinear
interpolation within a cell.
illustrates the geometry associated with bilinear
interpolation within a cell.

![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the approximation to the original
function surface that is implied by this method. For this set of
parameters it is a reasonable approximation of the original surface.
In general bilinear interpolation is a reasonable interpolation method
for sampling intervals up to about half of the Nyquist frequency. If the
data has high dips and high frequencies the approximation may not be
valid.
shows the approximation to the original
function surface that is implied by this method. For this set of
parameters it is a reasonable approximation of the original surface.
In general bilinear interpolation is a reasonable interpolation method
for sampling intervals up to about half of the Nyquist frequency. If the
data has high dips and high frequencies the approximation may not be
valid.