Next: CONCLUSIONS
Up: Biondi and Palacharla: 3-D
Previous: DERIVATION OF ROTATED McCLELLAN
We have tested the newly derived rotated McClellan filter
for depth extrapolating a 3-D wavefield
in a poststack migration program.
We migrated a band-limited (10-100 Hz) impulse delayed .48 seconds
assuming a constant propagation velocity of 2,250 meters per second.
The spatial sampling was 5 meters in both in-line and cross-line
directions and the depth step was constant for all frequencies
and equal to 5 meters.
The coefficients of the depth-extrapolation filters were
derived by windowing the ideal impulse response of the
operator with a Gaussian window Nautiyal et al. (1993).
To test the accuracy of the proposed method at high dips
we used a fairly long extrapolator with half-length
equal to 80 samples.
As explained in the previous section,
during the downward propagation we alternated
between depth steps
the application of
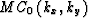 and
and 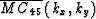 as transformation filters.
Further, we applied a spatial lowpass filter to the input data
to attenuate waves with wavenumbers
outside the circle defined by
as transformation filters.
Further, we applied a spatial lowpass filter to the input data
to attenuate waves with wavenumbers
outside the circle defined by 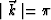 .These waves would be not correctly propagated in any case
because the McClellan transforms cause the replication of the extrapolation
operator along the radial directions in the wavenumber domain.
.These waves would be not correctly propagated in any case
because the McClellan transforms cause the replication of the extrapolation
operator along the radial directions in the wavenumber domain.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show respectively
the depth sections obtained by migrating the impulse using the
17-point McClellan filter
and the proposed averaged filter.
These sections were obtained by cutting the migrated cube along
one of the vertical diagonals; that is, along the direction with largest
error for both migration schemes.
Both sections show the typical semi-circular migration impulse
response; however the reflector computed using the
17-point filter is frequency dispersed above a depth of
about 300 meters, equivalent to a dip of about 55 degrees.
On the contrary, very little dispersion is present
in the result computed using the proposed method.
The reflector is correctly migrated up to the maximum dip
propagated by the extrapolator operator used for the test;
that is, a dip of about 78 degrees.
show respectively
the depth sections obtained by migrating the impulse using the
17-point McClellan filter
and the proposed averaged filter.
These sections were obtained by cutting the migrated cube along
one of the vertical diagonals; that is, along the direction with largest
error for both migration schemes.
Both sections show the typical semi-circular migration impulse
response; however the reflector computed using the
17-point filter is frequency dispersed above a depth of
about 300 meters, equivalent to a dip of about 55 degrees.
On the contrary, very little dispersion is present
in the result computed using the proposed method.
The reflector is correctly migrated up to the maximum dip
propagated by the extrapolator operator used for the test;
that is, a dip of about 78 degrees.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show
a depth slice of the migrated results, respectively computed
using the 17-point McClellan filter and the proposed filter.
The depth slices were cut at a depth of 200 meters,
equivalent to a dip of about 68 degrees.
The results of migration using the 17-point McClellan filter
are highly dispersed.
On the contrary,
the reflector migrated using the proposed method appears
to be perfectly circular, and very little dispersion of the
wavefield is present.
show
a depth slice of the migrated results, respectively computed
using the 17-point McClellan filter and the proposed filter.
The depth slices were cut at a depth of 200 meters,
equivalent to a dip of about 68 degrees.
The results of migration using the 17-point McClellan filter
are highly dispersed.
On the contrary,
the reflector migrated using the proposed method appears
to be perfectly circular, and very little dispersion of the
wavefield is present.
diagmcl17
Figure 4 Depth section along the diagonal direction of the impulse response of
3-D migration using 17-point McClellan filter.





diagnew
Figure 5 Depth section along the diagonal direction of the impulse response of
3-D migration using the proposed method.





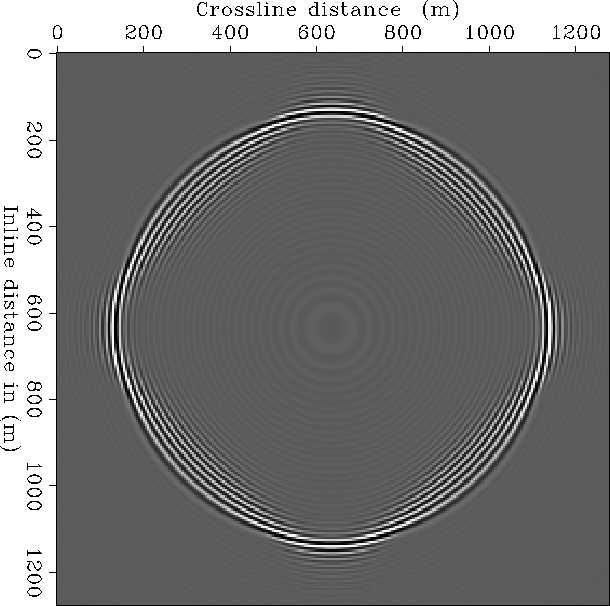
sli17
Figure 6 Depth slice of the impulse response of 3-D migration using 17-point
McClellan filter.





slinew
Figure 7 Depth slice of the impulse response of 3-D migration using
the proposed method.










Next: CONCLUSIONS
Up: Biondi and Palacharla: 3-D
Previous: DERIVATION OF ROTATED McCLELLAN
Stanford Exploration Project
11/17/1997
![]() and
and ![]() as transformation filters.
Further, we applied a spatial lowpass filter to the input data
to attenuate waves with wavenumbers
outside the circle defined by
as transformation filters.
Further, we applied a spatial lowpass filter to the input data
to attenuate waves with wavenumbers
outside the circle defined by ![]() .These waves would be not correctly propagated in any case
because the McClellan transforms cause the replication of the extrapolation
operator along the radial directions in the wavenumber domain.
.These waves would be not correctly propagated in any case
because the McClellan transforms cause the replication of the extrapolation
operator along the radial directions in the wavenumber domain.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show respectively
the depth sections obtained by migrating the impulse using the
17-point McClellan filter
and the proposed averaged filter.
These sections were obtained by cutting the migrated cube along
one of the vertical diagonals; that is, along the direction with largest
error for both migration schemes.
Both sections show the typical semi-circular migration impulse
response; however the reflector computed using the
17-point filter is frequency dispersed above a depth of
about 300 meters, equivalent to a dip of about 55 degrees.
On the contrary, very little dispersion is present
in the result computed using the proposed method.
The reflector is correctly migrated up to the maximum dip
propagated by the extrapolator operator used for the test;
that is, a dip of about 78 degrees.
show respectively
the depth sections obtained by migrating the impulse using the
17-point McClellan filter
and the proposed averaged filter.
These sections were obtained by cutting the migrated cube along
one of the vertical diagonals; that is, along the direction with largest
error for both migration schemes.
Both sections show the typical semi-circular migration impulse
response; however the reflector computed using the
17-point filter is frequency dispersed above a depth of
about 300 meters, equivalent to a dip of about 55 degrees.
On the contrary, very little dispersion is present
in the result computed using the proposed method.
The reflector is correctly migrated up to the maximum dip
propagated by the extrapolator operator used for the test;
that is, a dip of about 78 degrees.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and Figure
and Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show
a depth slice of the migrated results, respectively computed
using the 17-point McClellan filter and the proposed filter.
The depth slices were cut at a depth of 200 meters,
equivalent to a dip of about 68 degrees.
The results of migration using the 17-point McClellan filter
are highly dispersed.
On the contrary,
the reflector migrated using the proposed method appears
to be perfectly circular, and very little dispersion of the
wavefield is present.
show
a depth slice of the migrated results, respectively computed
using the 17-point McClellan filter and the proposed filter.
The depth slices were cut at a depth of 200 meters,
equivalent to a dip of about 68 degrees.
The results of migration using the 17-point McClellan filter
are highly dispersed.
On the contrary,
the reflector migrated using the proposed method appears
to be perfectly circular, and very little dispersion of the
wavefield is present.