Consider a porous medium whose connected pore space is saturated
with a single-phase viscous fluid. The fraction of total volume
occupied by fluid is the porosity , which is assumed to be
uniform on some appropriate length scale.
Bulk modulus and density of the fluid are Kf and ![]() ,respectively. Bulk and shear moduli of the drained porous frame are
Kd and .For simplicity, assume the frame is composed of a single
granular constituent whose bulk and shear moduli and density are
Km,
,respectively. Bulk and shear moduli of the drained porous frame are
Kd and .For simplicity, assume the frame is composed of a single
granular constituent whose bulk and shear moduli and density are
Km, ![]() , and
, and ![]() . Frame moduli may be measured
on drained samples, or may be estimated using one of
a variety of methods from the theory of composites (Berryman, 1980b,c;
Berryman and Milton, 1988).
. Frame moduli may be measured
on drained samples, or may be estimated using one of
a variety of methods from the theory of composites (Berryman, 1980b,c;
Berryman and Milton, 1988).
For long wavelength acoustic pulses (![]() where h is
a typical pore size) propagating through such a porous
medium, we define average values of local displacements
in the solid and also in the saturating fluid.
The average displacement vector in the solid frame is ,while that in the pore fluid is
where h is
a typical pore size) propagating through such a porous
medium, we define average values of local displacements
in the solid and also in the saturating fluid.
The average displacement vector in the solid frame is ,while that in the pore fluid is ![]() .A more useful way of quantifying fluid displacement is
to introduce the average displacement of fluid relative
to frame which is
.A more useful way of quantifying fluid displacement is
to introduce the average displacement of fluid relative
to frame which is ![]() .For small strains, frame dilatation is
.For small strains, frame dilatation is
e = .
Similarly, average fluid dilatation is
e_f = _f,
which includes fluid flow terms as well as dilatation. The increment of fluid content is defined by
= -= (e-e_f).
With these definitions, Biot (1956a,b;1962) introduces a quadratic strain-energy functional of the independent variables e and for an isotropic, linear porous medium
2E = He^2 - 2Ce+ M^2 - 4I_2,
where, if ![]() , then
I2 = exxeyy+eyyezz+ezzexx-exy2-eyz2-ezx2
is the second strain invariant (Berryman and Thigpen, 1985).
Elementary bounds on coefficients in the equations of
poroelasticity are presented by Thigpen and Berryman (1985).
Thermodynamic and mechanical stability require
non-negativity of E, which implies that
, then
I2 = exxeyy+eyyezz+ezzexx-exy2-eyz2-ezx2
is the second strain invariant (Berryman and Thigpen, 1985).
Elementary bounds on coefficients in the equations of
poroelasticity are presented by Thigpen and Berryman (1985).
Thermodynamic and mechanical stability require
non-negativity of E, which implies that ![]() ,
, ![]() ,
, ![]() ,and
,and ![]() . Then, components of the average stress tensor
for the saturated porous medium are
. Then, components of the average stress tensor
for the saturated porous medium are
_ij = [(H-2)e-C]_ij + 2e_ij, and fluid pressure pf is
Two coupled equations of motion for small disturbances in fluid-saturated media
may be derived easily from the energy functional E with these definitions of
stresses and pressures. With time dependence of the form ![]() ,Biot's equations of poroelasticity are, using the later notation of
Biot (1962),
,Biot's equations of poroelasticity are, using the later notation of
Biot (1962),
= _f + (1-)_m
and
q() = _f[/+ iF()/].
Tortuosity ![]() is a pure number related to frame inertia which has
been measured (Brown, 1980; Johnson et al., 1982) and can also be
estimated theoretically (Berryman, 1980a). Kinematic
viscosity of the saturating fluid is ; permeability of the porous frame
is ;
is a pure number related to frame inertia which has
been measured (Brown, 1980; Johnson et al., 1982) and can also be
estimated theoretically (Berryman, 1980a). Kinematic
viscosity of the saturating fluid is ; permeability of the porous frame
is ; ![]() is a dynamic viscosity factor proposed by Biot (1956b),
where
is a dynamic viscosity factor proposed by Biot (1956b),
where
![]() . The dynamic parameter h is a characteristic
length generally associated with steady-flow hydraulic radius of the pores,
or with a typical pore size.
. The dynamic parameter h is a characteristic
length generally associated with steady-flow hydraulic radius of the pores,
or with a typical pore size.
The coupled equations (Biot1) and (Biot2) give rise to three distinct modes of wave propagation: two compressional waves (with speeds v+ and vo for the faster and slower of the two wave speeds, respectively) and a single shear wave (with speed vs having two polarizations).
Coefficients appearing in Biot's equations of poroelasticity must be known before quantitative predictions can be made. Results of Brown and Korringa (1975) may be used to show that these coefficients are given for general isotropic porous media by
H = K_u + 43, where (using the definitions that follow) the undrained modulus Ku is determined by
K_s K_uK_s-K_u = K_s K_dK_s-K_d + K_K_f (K_-K_f), while the coefficients C and M are given by
C = (K_u - K_d)/ and M = C/, with
= 1 - K_d/K_s. The three bulk moduli characteristic of the drained porous frame are defined by Brown and Korringa (1975) through the expressions:
1K_ = - 1V_(V_p_f)_p_d,
where V is total sample volume, ![]() is pore volume,
is pore volume,
![]() is external (confining) pressure,
pf is pore pressure, and pd = pc - pf is differential pressure.
Brown and Korringa (1975) state that, although these
three bulk moduli have simple physical interpretations,
this ``does not necessarily help in knowing their values.''
Observing the change in pore volume (an internal variable) required by
(Kpore) is clearly more difficult than observing the change in total
sample volume (an external variable) required by the other two moduli.
Nevertheless, all three moduli may, in principle, be measured in quasi-static
measurements, thus determining their values directly. However, it is
commonly the case that acoustic measurements are made on compressional and
shear wave speeds in fluid saturated porous media. It would therefore be
beneficial to have a means of deducing these constants from wave data.
is external (confining) pressure,
pf is pore pressure, and pd = pc - pf is differential pressure.
Brown and Korringa (1975) state that, although these
three bulk moduli have simple physical interpretations,
this ``does not necessarily help in knowing their values.''
Observing the change in pore volume (an internal variable) required by
(Kpore) is clearly more difficult than observing the change in total
sample volume (an external variable) required by the other two moduli.
Nevertheless, all three moduli may, in principle, be measured in quasi-static
measurements, thus determining their values directly. However, it is
commonly the case that acoustic measurements are made on compressional and
shear wave speeds in fluid saturated porous media. It would therefore be
beneficial to have a means of deducing these constants from wave data.
Constant Kd is the (jacketed) bulk modulus of the drained porous frame,
and is commonly measured since it is precisely what one would think of
as the bulk modulus of the dry (or drained) rock in nonporous elasticity.
However, values of the two remaining constants Ks (the unjacketed modulus)
and ![]() (the unjacketed pore modulus) are not generally known or
measured unless the porous frame is homogeneous on the microscopic scale.
For this special circumstance [which is also the only one considered
explicitly by Gassmann (1951)] with a single type of elastic solid composing
the frame, these two moduli both equal the bulk modulus Km
of the single granular constituent
(the unjacketed pore modulus) are not generally known or
measured unless the porous frame is homogeneous on the microscopic scale.
For this special circumstance [which is also the only one considered
explicitly by Gassmann (1951)] with a single type of elastic solid composing
the frame, these two moduli both equal the bulk modulus Km
of the single granular constituent
K_s = K_= K_m. Thus, Gassmann's equation is equivalent to
1M = K_f + -K_m, = 1 - K_d/K_m, while Brown and Korringa's more general result (undrained) may be rearranged to show that
1M = K_f + K_s - K_,
= 1 - K_d/K_s.
Note the important fact (to be used later) that the theory clearly shows
1/M is always a linear function of the fluid compressibility ![]() .Gassmann's result (Gassmanns) has also been derived within the context of
Biot's theory of poroelasticity by Biot and Willis (1957) and by Geertsma
(1957). Geertsma and Smit (1962) discuss practical aspects of applications
of the theory to rocks. Rice (1975) and Rice and Cleary (1976) also obtain
a general result
essentially equivalent to that of Brown and Korringa (BandKs).
.Gassmann's result (Gassmanns) has also been derived within the context of
Biot's theory of poroelasticity by Biot and Willis (1957) and by Geertsma
(1957). Geertsma and Smit (1962) discuss practical aspects of applications
of the theory to rocks. Rice (1975) and Rice and Cleary (1976) also obtain
a general result
essentially equivalent to that of Brown and Korringa (BandKs).
The more general constants of Brown and Korringa, Ks and ![]() ,must somehow be related to material properties of multiple solid
constituents of the porous frame. Equation (BandKs) provides a
possible method of determining the constants as we will show:
by saturating the same porous medium with different pore fluids, it
should therefore be possible to deduce the values of the frame moduli from
the variations in M with fluid compressibility.
,must somehow be related to material properties of multiple solid
constituents of the porous frame. Equation (BandKs) provides a
possible method of determining the constants as we will show:
by saturating the same porous medium with different pore fluids, it
should therefore be possible to deduce the values of the frame moduli from
the variations in M with fluid compressibility.
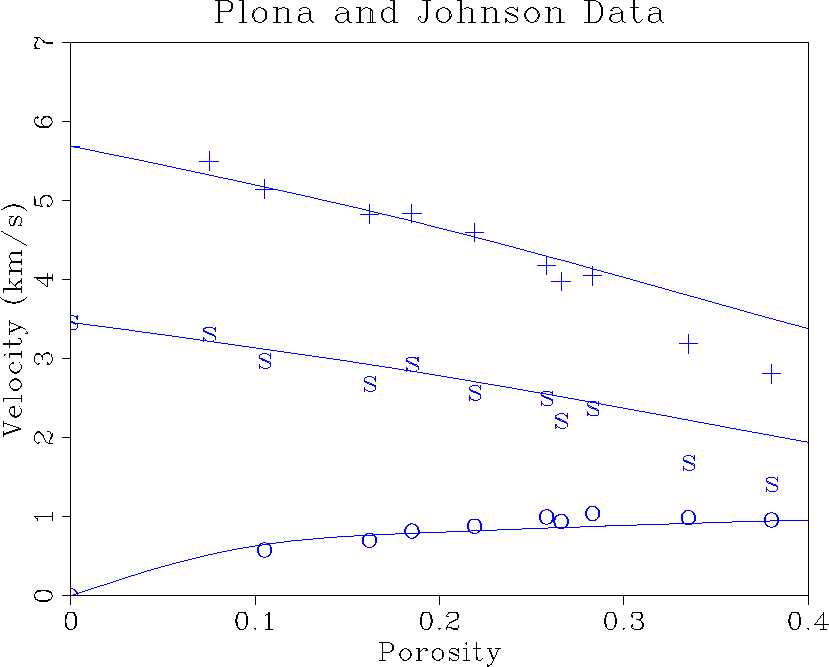
Before attacking the inversion problem, we first show an example illustrating the success of the theory in predicting the results of certain wave propagation experiments.
 |