




Next: Conclusions
Up: SYNTHETIC TESTS
Previous: SYNTHETIC TESTS
As mentioned earlier, least-squares Kirchhoff migration
involves using only a single slice out of a much larger
transform domain cube. If the rest of the cube contained
no interesting information, then the extra computations
of the least-squares method would not be justified. However,
the rest of the transform domain cube does serve a purpose.
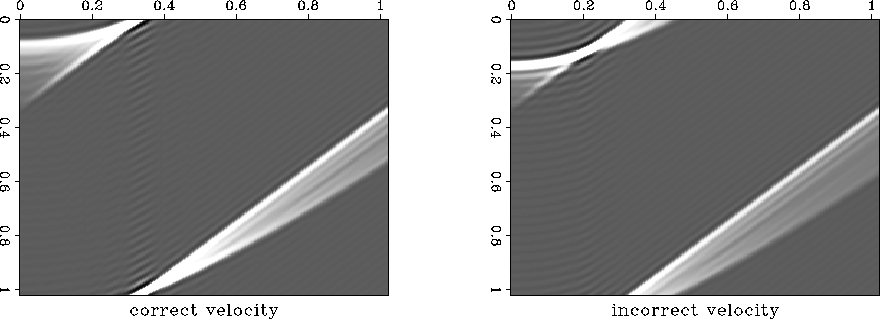
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a single slice taken from two
such cubes. This is for a non least-squares example.
The x coordinate is fixed at the location
of the single point scatterer; the axes are t and t0.
The cube has been shifted so that the single slice that
corresponds to the migrated image lies along the top of
the cube. On the left is the result of migrating with the
correct constant velocity; we see energy focusing near the
top of the plot. On the right is the result of migrating
with too high a velocity (3.5 km/sec instead of 3 km/sec).
The focusing of energy away from the t=t0 plane tells
us that an incorrect migration velocity was used. The
cube contains important information, similar to a
migration velocity analysis, away from the image plane.
This gives us reason to think that the added cost of the least-squares
method might be worthwhile.
focus
shows a single slice taken from two
such cubes. This is for a non least-squares example.
The x coordinate is fixed at the location
of the single point scatterer; the axes are t and t0.
The cube has been shifted so that the single slice that
corresponds to the migrated image lies along the top of
the cube. On the left is the result of migrating with the
correct constant velocity; we see energy focusing near the
top of the plot. On the right is the result of migrating
with too high a velocity (3.5 km/sec instead of 3 km/sec).
The focusing of energy away from the t=t0 plane tells
us that an incorrect migration velocity was used. The
cube contains important information, similar to a
migration velocity analysis, away from the image plane.
This gives us reason to think that the added cost of the least-squares
method might be worthwhile.
focus
Figure 9 Left, migration with correct velocity.
Slice for a single x coordinate, at the scatterer location.
Focus is on the t=t0 line, which has been shifted to lie along
the top of the plot.
Right, migration with incorrect velocity gives focus that is
away from the t=t0 line.






Next: Conclusions
Up: SYNTHETIC TESTS
Previous: SYNTHETIC TESTS
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a single slice taken from two
such cubes. This is for a non least-squares example.
The x coordinate is fixed at the location
of the single point scatterer; the axes are t and t0.
The cube has been shifted so that the single slice that
corresponds to the migrated image lies along the top of
the cube. On the left is the result of migrating with the
correct constant velocity; we see energy focusing near the
top of the plot. On the right is the result of migrating
with too high a velocity (3.5 km/sec instead of 3 km/sec).
The focusing of energy away from the t=t0 plane tells
us that an incorrect migration velocity was used. The
cube contains important information, similar to a
migration velocity analysis, away from the image plane.
This gives us reason to think that the added cost of the least-squares
method might be worthwhile.
shows a single slice taken from two
such cubes. This is for a non least-squares example.
The x coordinate is fixed at the location
of the single point scatterer; the axes are t and t0.
The cube has been shifted so that the single slice that
corresponds to the migrated image lies along the top of
the cube. On the left is the result of migrating with the
correct constant velocity; we see energy focusing near the
top of the plot. On the right is the result of migrating
with too high a velocity (3.5 km/sec instead of 3 km/sec).
The focusing of energy away from the t=t0 plane tells
us that an incorrect migration velocity was used. The
cube contains important information, similar to a
migration velocity analysis, away from the image plane.
This gives us reason to think that the added cost of the least-squares
method might be worthwhile.