The tree as a root-generating algorithm

Looking at the roots of sequences of polynomials is always interesting, and our sequence of filters just described is no exception. Again, Mallat's Tree can be used with these three rules:

• Convolving two polynomials is equivalent to forming the union of their roots.
• Filtering decimated data is equivalent to filtering the undecimated data with a zero-padded filter followed by decimating the output.
• The roots of a filter zero-padded between every coefficient are the square roots of the roots of the same unpadded filter.

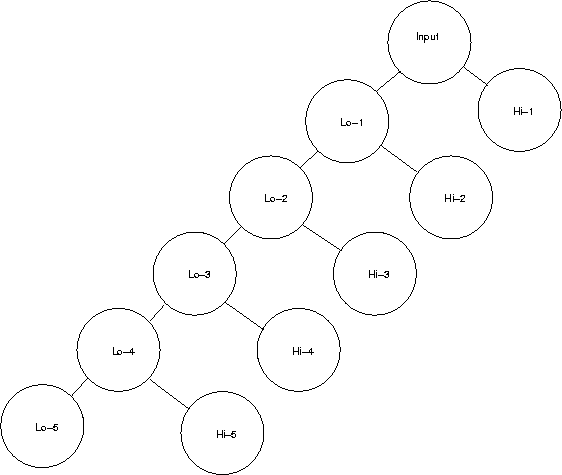
With these rules in place, the roots of the new low-pass filter are the roots of the old low-pass filter in union with the roots of the basic low-pass wavelet zero-padded by the number of stages. This is illustrated in Figures and .

 

tree
Figure 11 Mallat's tree.

 

haarwave
Figure 12 The wavelets and the zeros for the Haar wavelets. In each plot, the top row shows the high-pass Haar wavelet on the left and its zeros on the complex plane on the right. The bottom row shows the low-pass Haar wavelet and its zeros. Multiple zeros have multiple circles drawn around them. In the electronic version of this paper, pressing the button starts a movie of these figures.

 

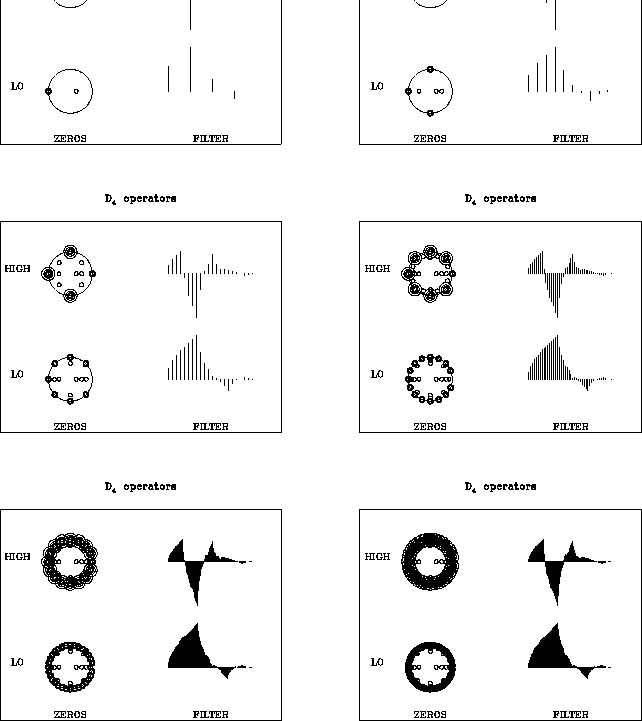
wave
Figure 13 The wavelets and the zeros for various forms of D₄. In each plot, the top row shows the high-pass D₄ wavelet on the left and its zeros on the complex plane on the right. The bottom row shows the low-pass D₄ wavelet and its zeros. Multiple zeros have multiple circles drawn around them. In the electronic version of this paper, pressing the button starts a movie of these figures.