THE MODIFIED WAVE EQUATION

Since the numerical solution is an approximation of the exact solution, it does not exactly satisfy the continuous partial differential equation at hand, but it satisfies a modified equation. In this case, I use the Crank-Nicolson method to solve the diffraction equation

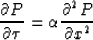$${\partial P\over \partial \tau } = \alpha {{\partial}^2 P\over \partial x^2}$$ (32)

$${ {P^{(n+1)}-P^{(n)}}\over {\Delta \tau}} = {\alpha \over 2}... ...partial x^2} + {{\partial}^2 P^{(n)}\over \partial x^2} \right]$$ (33)

$${ {P^{(n+1)}_{j}-P^{(n)}_{j}}\over {\Delta \tau}} = {\alpha ... ...)}_{j+1}-2P^{(n)}_{j}+P^{(n)}_{j-1}}\over {\Delta x^2}} \right]$$ (34)

By Taylor series expansion of every term about Pⁿ_j, I obtain the modified wave equation that the numerical solution actually satisfies:

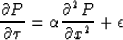$${\partial P\over \partial \tau } = \alpha {{\partial}^2 P\over \partial x^2} + \epsilon$$ (35)

$$\epsilon = { {\alpha \Delta x^2}\over 12} {{\partial}^4 P\ov... ...2 {\alpha}^2 \right] {{\partial}^6 P\over \partial x^6}+ \ldots$$ (36)

The error term shows that the trace spacing interval 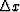$\Delta x$ plays a larger role than the depth step size 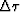$\Delta \tau$of downward continuation in determining the accuracy of the numerical solution.