




Next: THE MODIFIED WAVE EQUATION
Up: OVERMIGRATION CAUSED BY THE
Previous: OVERMIGRATION CAUSED BY THE
The most popularly used numerical method of solving a stiff system of ODEs
such as (11) is the Crank-Nicolson method, chosen because of its
unconditional stability and good accuracy.
First let us look at the Crank-Nicolson (trapezoidal) method
for a single first-order ODE.
Applying the Crank-Nicolson method to the model equation
| 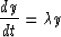 |
(21) |
yields
| 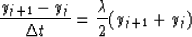 |
(22) |
or
| 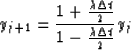 |
(23) |
Thus the solution of (21) can be written as
| 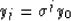 |
(24) |
where y0 is the initial condition and
| 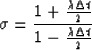 |
(25) |
For the migration wavefield extrapolation equation (19), the eigenvalue
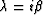 (
(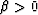 ) is purely
imaginary. Thus
) is purely
imaginary. Thus
| 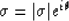 |
(26) |
Because 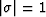 , the Crank-Nicolson method as applied to
migration wavefield
extrapolation does not generate any amplitude error.
This result agrees with the
one-way migration wavefield extrapolation that is a dampless sinusoidal
wave propagation. However, there is phase error. The numerical solution is
, the Crank-Nicolson method as applied to
migration wavefield
extrapolation does not generate any amplitude error.
This result agrees with the
one-way migration wavefield extrapolation that is a dampless sinusoidal
wave propagation. However, there is phase error. The numerical solution is
| 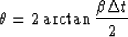 |
(27) |
| 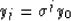 |
(28) |
| 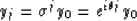 |
(29) |
But the exact solution of the ODE (21) is
| 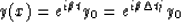 |
(30) |
The phase error is
| 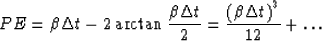 |
(31) |
The numerical solution lags behind the exact solution.
Thus applying the Crank-Nicolson method to the diffraction
equation causes overmigration - the experimental error.
And the eigenvalues with larger moduli have larger degrees of overmigration.





Next: THE MODIFIED WAVE EQUATION
Up: OVERMIGRATION CAUSED BY THE
Previous: OVERMIGRATION CAUSED BY THE
Stanford Exploration Project
11/17/1997
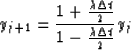
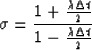
![]() (
(![]() ) is purely
imaginary. Thus
) is purely
imaginary. Thus