To introduce datuming that uses a finite-difference method, let me
first describe datuming from a lower planar datum to a higher planar datum.
A scatterer is located at (z=0.15, y=0.32) in a constant velocity
v=1 medium. The variables z and y denote depth and horizontal coordinates.
I generate the synthetic zero-offset section in Figure 1
at the planar datum z=0.05 by ray tracing, for which only the traveltime is
correct.
The apex of the hyperbola is at time t=0.1.
Then I use a grid in which
nz=20, ny=128, dz=0.005, dy=0.005, and dt=0.001 to run the
two-way wave equation forward in time
with the synthetic record as the boundary condition
at the lower recording datum.
The desired wavefields at the higher planar datum
are the absorbing history wavefields at the top iz=1 of the grid,
or the history wavefields at the planar datum
just one grid point below the top, so that the absorbing boundary conditions
can be implemented efficiently.
The results are shown in Figure 2.
In this case, the datuming is done over 50 m.
After the datuming process, the apex of the hyperbola is at time t=0.15.
The time period for running the wave equation
must be larger than the original record length by an amount
that is long enough
to account for the propagation time from the lower datum to the
higher datum, because the actual earth wavefields expand up from
the subsurface.
There is a light ghost following the main event, which results
from the reverberations between the input datum and the output datum.
The ghost reflection can be removed by implementing better absorbing boundary
conditions at the output datum, and implementing the recorded wavefields
as a series of point sources instead of simple boundary conditions.
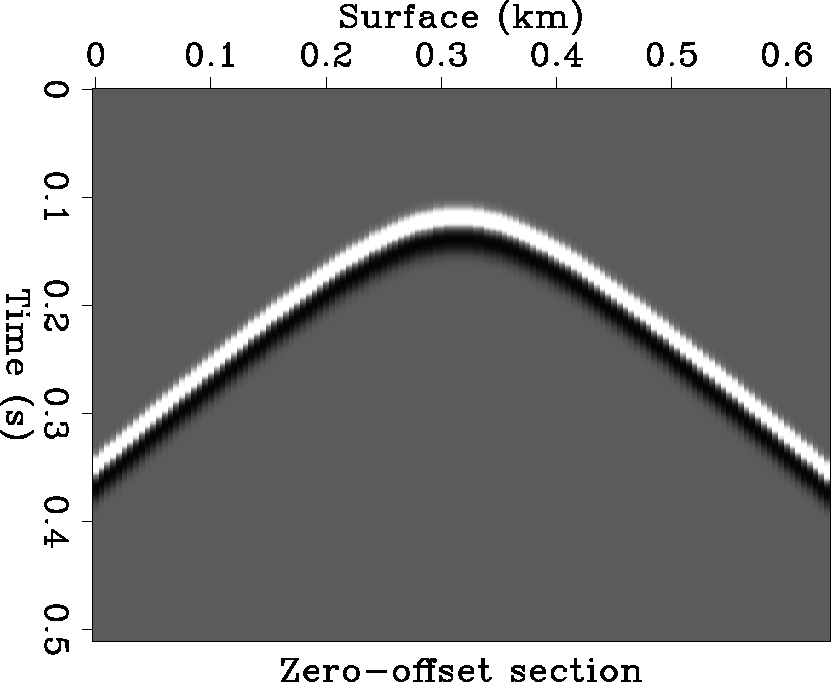d1
Figure 1 The wavefields recorded
at the planar datum z=0.05
d1.2
Figure 2 The extrapolated wavefields
at the upper planar datum z=0.
The apex of the hyperbola has been shifted by the datuming.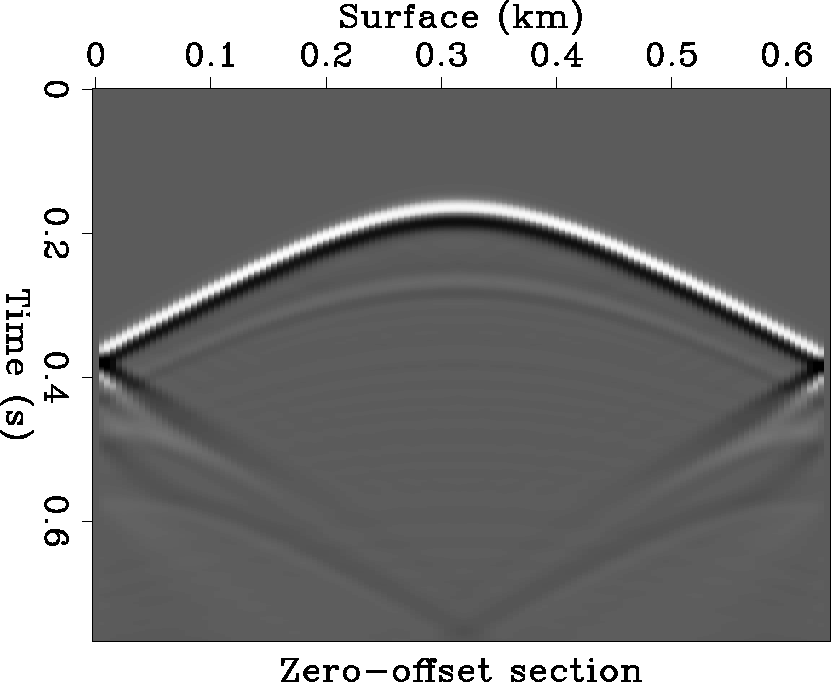
